Solución
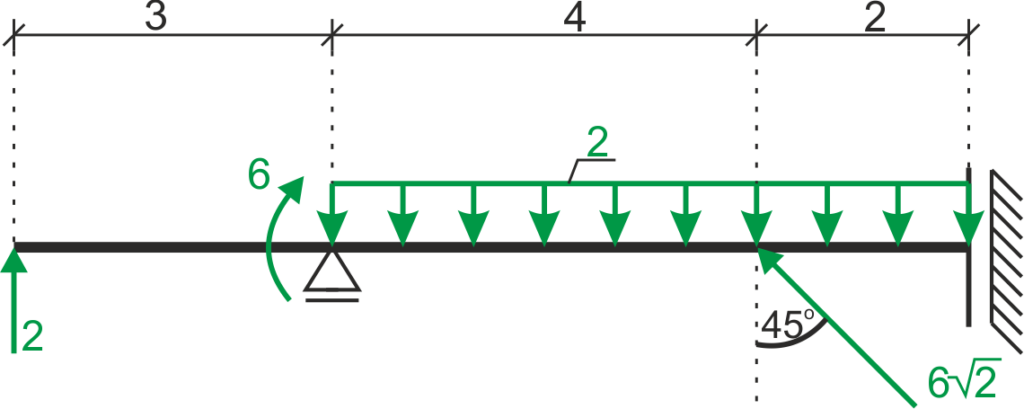
1. Designation of characteristic points and reactions at supports

2. Calculation of reactions using equilibrium equations
\begin{aligned} &\sum X=0 \\ &-6+H_{D}=0 \\ &H_{D}=6 k N \\ &\sum Y=0 \\ &2-2 \cdot 6+6+V_{B}=0 \\ &B_{B}=4 k N \\ &\sum M_{B}=0 \\ &2 \cdot 3+6-6 \cdot 4+6 \cdot 2 \cdot 3-M_{D}=0 \\ &M_{D}=24 k N \end{aligned}3. Writing equations for internal forces in individual variable intervals:
a) Interval AB 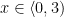
 \begin{aligned}
&Q_{AB}=2 \ kN\\
&M_{AB}=2x\\
&M_{A}(0)=0\\
&M_{B}(3)=6 \ kNm\\
\end{aligned}
\begin{aligned}
&Q_{AB}=2 \ kN\\
&M_{AB}=2x\\
&M_{A}(0)=0\\
&M_{B}(3)=6 \ kNm\\
\end{aligned}
b) Interval BC 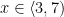
 \begin{aligned}
&Q_{BC}=2 + 4 – 2(x-3)\\
&M_{BC}=2x + 4(x-3) + 6 – \frac{1}{2}\cdot 2(x-3)^{2}\\
&Q_{B}(3)=6 \ kN\\
&Q_{C}(7)=2 \ kN\\
&Q_{BC}=0\\
&6-2(x-3)=0\\
&6-2x + 6=0\\
&x=6\\
&M_{B}(3)=12 \ kNm\\
&M_{max}(6)=21 \ kNm\\
&M_{C}(7)=20 \ kNm\\
\end{aligned}
\begin{aligned}
&Q_{BC}=2 + 4 – 2(x-3)\\
&M_{BC}=2x + 4(x-3) + 6 – \frac{1}{2}\cdot 2(x-3)^{2}\\
&Q_{B}(3)=6 \ kN\\
&Q_{C}(7)=2 \ kN\\
&Q_{BC}=0\\
&6-2(x-3)=0\\
&6-2x + 6=0\\
&x=6\\
&M_{B}(3)=12 \ kNm\\
&M_{max}(6)=21 \ kNm\\
&M_{C}(7)=20 \ kNm\\
\end{aligned}
c) Interval DC 
 \begin{aligned}
&Q_{DC}=2x\\
&Q_{D}(0)=0\\
&Q_{C}(2)=4 \ kN\\
&M_{DC}=24 – 2x\frac{x}{2}=24 – x^{2}\\
&M_{D}(0)=24 \ kNm\\
&M_{C}(2)=20 \ kNm\\
&N_{DC}=6 \ kN\\
\end{aligned}
\begin{aligned}
&Q_{DC}=2x\\
&Q_{D}(0)=0\\
&Q_{C}(2)=4 \ kN\\
&M_{DC}=24 – 2x\frac{x}{2}=24 – x^{2}\\
&M_{D}(0)=24 \ kNm\\
&M_{C}(2)=20 \ kNm\\
&N_{DC}=6 \ kN\\
\end{aligned}
4. Final diagrams

Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.