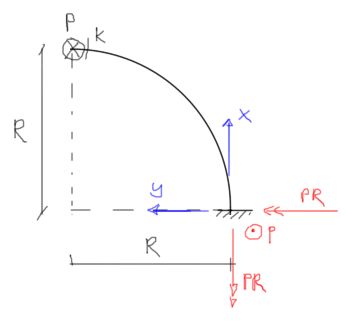
En el estado P, las reacciones y las fórmulas para las fuerzas internas son:

\begin{aligned} &M_{g}=-P \cdot R \cdot \sin (\alpha) \\ &M_{s}=P \cdot R \cdot(1-\cos (\alpha)) \end{aligned}

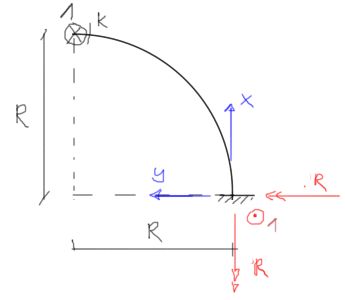
En el estado unitario, las reacciones y las fórmulas para las fuerzas internas son:

\begin{aligned} &m_{g}=-R \cdot \sin (\alpha) \\ &m_{s}=R \cdot(1-\cos (\alpha)) \end{aligned}

Calculo la desplazamiento del punto K usando la fórmula Maxwell Mohra:

\begin{aligned} &y=\frac{1}{E I} \int_{0}^{\frac{\pi}{2}}(-P \cdot R \cdot \sin (\alpha)) \cdot(-R \cdot \sin (\alpha)) \mathrm{d} \alpha+\frac{1}{G I} \int_{0}^{\frac{\pi}{2}} P \cdot R \cdot(1-\cos (\alpha)) \cdot R \cdot(1-\cos (\alpha)) \mathrm{d} \alpha \\ &y=\frac{1}{E I} \int_{0}^{\frac{\pi}{2}} P \cdot R^{2} \cdot \sin (\alpha)^{2} \mathrm{~d} \alpha+\frac{1}{G I} \int_{0}^{\frac{\pi}{2}} P \cdot R^{2} \cdot(\cos (\alpha)-1)^{2} \mathrm{~d} \alpha \end{aligned}

Donde los valores de cada integral son:

\begin{aligned} &\int_{0}^{\frac{\pi}{2}} P \cdot R^{2} \cdot \sin (\alpha)^{2} \mathrm{~d} \alpha \rightarrow \frac{P \cdot R^{2} \cdot \pi}{4} \\ &\frac{\pi}{2} \\ &\int_{0} P \cdot R^{2} \cdot(\cos (\alpha)-1)^{2} \mathrm{~d} \alpha \rightarrow \frac{3 \cdot P \cdot R^{2} \cdot \pi}{4}-2 \cdot P \cdot R^{2} \end{aligned}

Por lo tanto, finalmente

\begin{aligned} y=\frac{7 \cdot P \cdot R^{2} \cdot \pi}{4}-4 \cdot P \cdot R^{2} \end{aligned}