Solución
1. Determinación del grado de indeterminación cinemática:
\begin{aligned} &SKN=1\\ \end{aligned}2. Selección del sistema base del método de desplazamientos (UPMP):
3. Gráficos y determinación de los coeficientes y términos independientes de la ecuación:
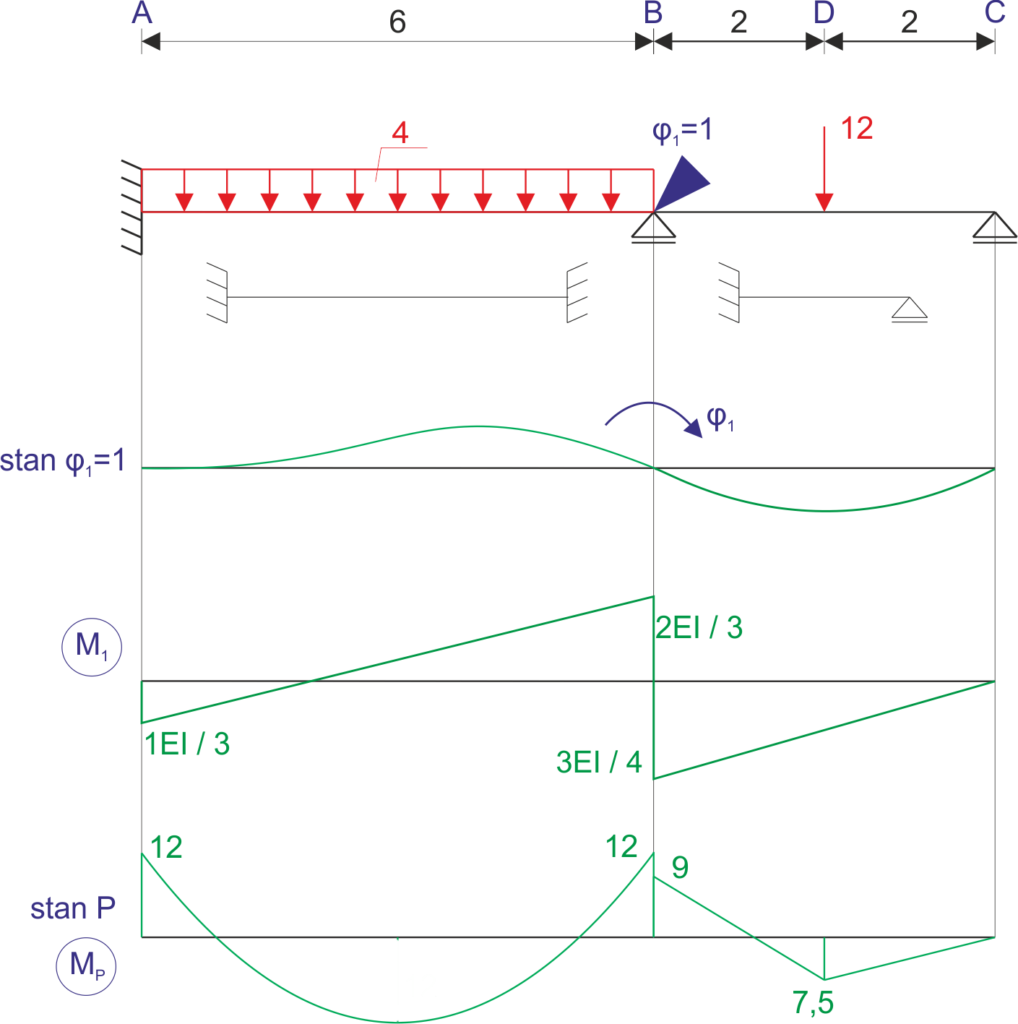
Determinación de los coeficientes del UPMP
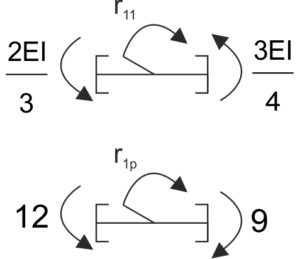 \begin{aligned}
&r_{11}=\frac{2EI}{3} +\frac{3EI}{4} =\frac{17EI}{12}\\
&r_{1p}=12-9=3\\
\end{aligned}
\begin{aligned}
&r_{11}=\frac{2EI}{3} +\frac{3EI}{4} =\frac{17EI}{12}\\
&r_{1p}=12-9=3\\
\end{aligned}
Sistema de ecuaciones:
\begin{aligned} &r_{11}\cdot\varphi_{1} +r_{1p}=0\\ \end{aligned} \begin{aligned} &\varphi_{1}=-\frac{r_{1p}}{r_{11}}=-\frac{36}{17EI}\\ \\ &M_{ost}=M_{p}+\varphi_{1}\cdot M_{1}\\ &M_{AB}=-12-\frac{1}{3}\cdot \left(-\frac{36}{17}\right)=-12,706\\ &M_{BA}=12+\frac{2}{3}\cdot \left(-\frac{36}{17}\right)=-10,588\\ &M_{BC}=-9+\frac{3}{4}\cdot \left(-\frac{36}{17}\right)=-10,588\\ &M_{CB}=0\\ \end{aligned}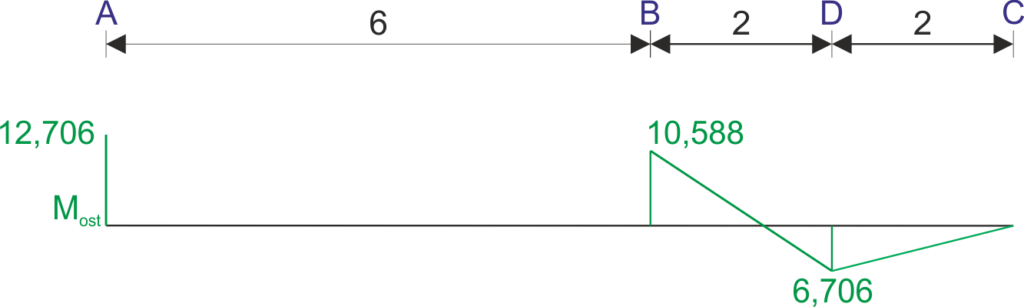
Elemento AB:
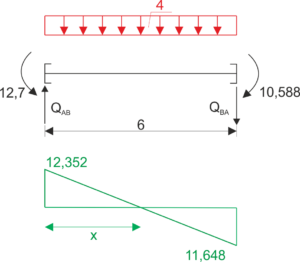 \begin{aligned}
&\sum{M_{B}}=0\\
&{Q_{AB}}\cdot 6+10,588-12,7-4\cdot6\cdot3=0\\
&{Q_{AB}}=12,352\\
&\sum{M_{A}}=0\\
&{Q_{BA}}\cdot 6+10,588+4\cdot 6\cdot 3-12,7=0\\
&{Q_{BA}}=-11,648\\
&\frac{12,352}{x}=\frac{11,648}{6-x}\\
&74,112-12,352x=11,648\\
&x=3,088\\
&M_{max}=-12,7+0,5\cdot 12,352\cdot 3,088\\
\end{aligned}
\begin{aligned}
&\sum{M_{B}}=0\\
&{Q_{AB}}\cdot 6+10,588-12,7-4\cdot6\cdot3=0\\
&{Q_{AB}}=12,352\\
&\sum{M_{A}}=0\\
&{Q_{BA}}\cdot 6+10,588+4\cdot 6\cdot 3-12,7=0\\
&{Q_{BA}}=-11,648\\
&\frac{12,352}{x}=\frac{11,648}{6-x}\\
&74,112-12,352x=11,648\\
&x=3,088\\
&M_{max}=-12,7+0,5\cdot 12,352\cdot 3,088\\
\end{aligned}
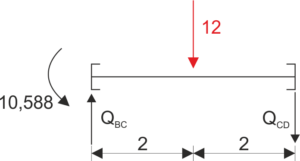
Elemento BD:
 \begin{aligned}
&\sum{M_{C}}=0\\
&{Q_{BC}}\cdot 4-12\cdot 2-10,588=0\\
&{Q_{BC}}=8,647\\
&\sum y=0\\
&8,647-12-Q_{CD}=0\\
&Q_{CD}=-3,353\\
\end{aligned}
\begin{aligned}
&\sum{M_{C}}=0\\
&{Q_{BC}}\cdot 4-12\cdot 2-10,588=0\\
&{Q_{BC}}=8,647\\
&\sum y=0\\
&8,647-12-Q_{CD}=0\\
&Q_{CD}=-3,353\\
\end{aligned}
Gráficos finales de las fuerzas internas
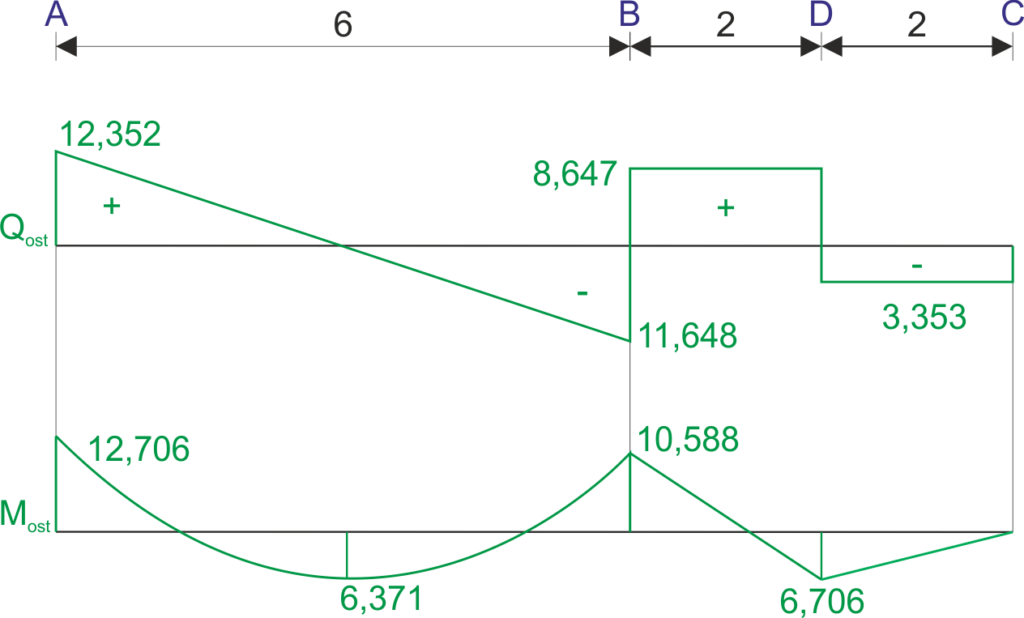
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.
