See the theoretical introduction to the Maxwell-Mohr method! Also, check out more on integration using the Wereszczagin method.

Problem solution:

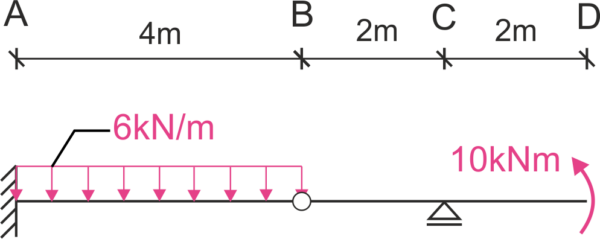
We break down the hinged beam into simple beams, calculate the support reactions, and draw internal force diagrams. Note that the reactions can be calculated without breaking down the beam. Calculating the maximum or minimum value is not necessary for calculating the displacement.

\begin{array}{cl} \mathbb{I} & \\ \sum M_{B}=0 & 10+2 V_{C}=0 \\ & V_{C}=-5 \mathrm{kN} \\ \sum Y=0 & V_{B}+V_{C}=0 \\ & V_{B}=5 \mathrm{kN} \end{array} \begin{aligned} \frac{29}{x}=\frac{29+5}{4}=>x=\frac{29 \cdot 4}{29+5}=\frac{58}{17} \approx 3.412 \end{aligned} \begin{array}{ll} \sum M_{A}=0 & -M_{A}-6 \cdot 4 \cdot 2-4 V_{B}=0 \\ & M_{A}=-68 \mathrm{kNm} \\ \sum Y=0 & V_{A}-6 \cdot 4-V_{B}=0 \\ & V_{A}=29 \mathrm{kN} \end{array} \begin{array}{cl} \mathbb{I} & \\ \sum M_{B}=0 & -1 \cdot 4+2 V_{C}=0 \\ & V_{C}=2 \mathrm{kN} \\ \sum Y=0 & V_{B}+V_{C}-1=0 \\ & V_{B}=-1 \mathrm{kN} \end{array} \begin{array}{ll} \mathbb{II} & \\ \sum M_{A}=0 & -M_{A}-4 V_{B}=0 \\ & M_{A}=4 \mathrm{kNm} \\ \sum Y=0 & V_{A}-V_{B}=0 \\ & V_{A}=1 \mathrm{kN} \end{array}

We calculate the displacement taking into account the dominant bending moment and the shear force. If we don't have numerical data, we leave the result in the form shown below.

\begin{aligned} \Delta_{D}=& \int \frac{M_{P} M_{1}}{E I} d x+\kappa \int \frac{Q_{P} Q_{1}}{G A}=\\ =& \frac{1}{E I}\left[-\frac{1}{3} \cdot 4 \cdot 68 \cdot 4+\frac{1}{3} \cdot 4 \cdot 4 \cdot \frac{6 \cdot 4^{2}}{8}-\frac{1}{3} \cdot 2 \cdot 2 \cdot 10-\frac{1}{2} \cdot 2 \cdot 2 \cdot 10\right]+\\ &+\frac{\kappa}{G A}\left[-\frac{1}{2} \cdot 2 \cdot 29 \cdot 1+\frac{1}{3} \cdot 4 \cdot 5 \cdot 1+2 \cdot 1 \cdot 5\right]=\\ =&-332 \frac{1}{E I}-\frac{124}{3} \frac{\kappa}{G A} \end{aligned}