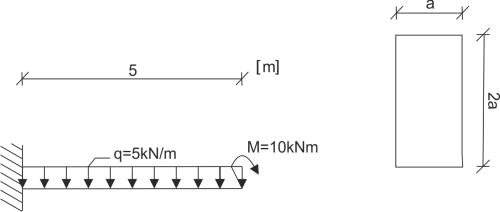
Solution
The maximum deflection will be at the free end of the beam. To calculate it, we will use the Clebsch's method.
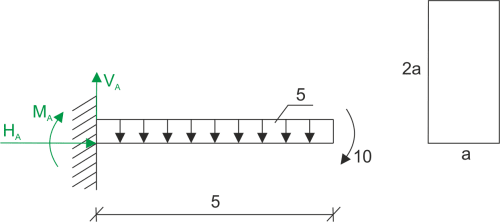 \begin{aligned} &\sum{y}=0\\ &V_{A}-25=0\\ &V_{A}=25\ kN\\ &\sum{M_A}=0\\ &M_{u}+10+5\cdot 5\cdot 2.5=0\\ &M_{u}=-72.5\ kNm\\ \end{aligned}
\begin{aligned} &\sum{y}=0\\ &V_{A}-25=0\\ &V_{A}=25\ kN\\ &\sum{M_A}=0\\ &M_{u}+10+5\cdot 5\cdot 2.5=0\\ &M_{u}=-72.5\ kNm\\ \end{aligned}
The moment of inertia of the cross-section and the moment function for the beam (expressed on the left side).
\begin{aligned} &I_{yc}=\frac{a\cdot (2a)^3}{12}=\frac{2}{3}a^4\\ &EIw ''=-Mg\\ &Mg=V_{A}x+M_A\cdot x^0-\frac{1}{2}qx^2\\ &EIw''=-25x+72.5x^0+2.5x^2\\ &EIw'=-25\frac{x^2}{2}+72.5x+2.5\frac{x^3}{3}+C\\ &EIw=-25\frac{x^3}{6}+72.5\frac{x^2}{2}+2.5\frac{x^4}{12}+Cx+D\\ \end{aligned}Boundary conditions
\begin{aligned} &w'(0)=0\\ &C=0\\ &w(0)=0\\ &D=0\\ &w_{max}=\frac{w(5)}{EI}=\frac{-25\frac{5^3}{6}+72.5\cdot \frac{5^2}{2}+2.5\frac{5^4}{12}}{EI}=\frac{515.625}{EI}\\ \end{aligned}Condition from the problem description
\begin{aligned} &w_{max}\le w_{dop}\\ \\ &\frac{515.625\cdot 10^3}{200\cdot 10^9\cdot \frac{2}{3}a^4}\le 0.01\\ \\ &a\ge 0.14\ m\\ &a=15\ cm\\ \end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.