Solution
Classic Solution
Casting the force in bar AC into horizontal and vertical components.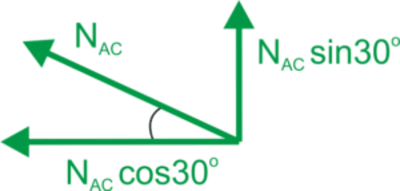
Equations of static equilibrium for node A. \begin{aligned} &\sum{Y}=0\\ &N_{AC}\cdot\sin30^{o}=0\\ &N_{AC}=2G\\ &\sum{X}=0\\ &-N_{AB}-N_{AC}\cdot\cos30^{o}=0\\ &N_{AB}=-2G\cdot\frac{\sqrt3}{2}\\ &N_{AB}=-G\sqrt3\\ \end{aligned} Strength condition
We mark the elongation and contraction of bars (along their axes).
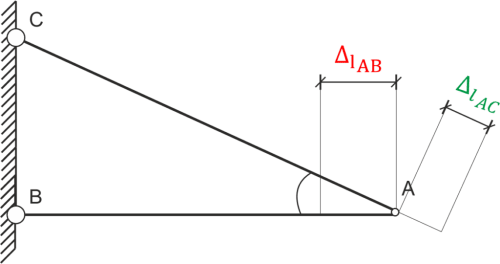
We calculate the elongation of bar AC (positive force in the bar) and the contraction of bar AB (negative force - compressed bar). \begin{aligned} \Delta l &= \frac{Nl}{EA} \\ \Delta l_{AB} &= \frac{-50 \cdot \sqrt{3} \cdot 10^{3} \cdot 1.2}{E_{m} \cdot a^{2}} = \frac{-50 \cdot \sqrt{3} \cdot 10^{3} \cdot 1.2}{1.15 \cdot 10^{11} \cdot 0.047^{2}} = -4.09 \times 10^{-4} \ m = -0.409 \ mm \end{aligned} We calculate the length of bar AC and its elongation. \begin{aligned} &\frac{1.2}{|AC|}=\cos30^{o} & \\ & |AC|=\frac{1.2}{\cos30^{o}}=1.386\\ &\Delta l_{AC}=\frac{50\cdot 2\cdot 10^{3}\cdot |AC|}{E_{s}\cdot\frac{\pi d^{2}}{4}}=\frac{50\cdot 2\cdot 10^{3}\cdot 1.386\cdot 4}{2.1\cdot 10^{11}\cdot\pi\cdot 0.03^{2}}=9.337\cdot 10^{-4} \ m=0.934 \ mm\\ \end{aligned} We mark the permitted line of elongation/contraction displacements of bars and find their intersection - this is the final displacement of point A.
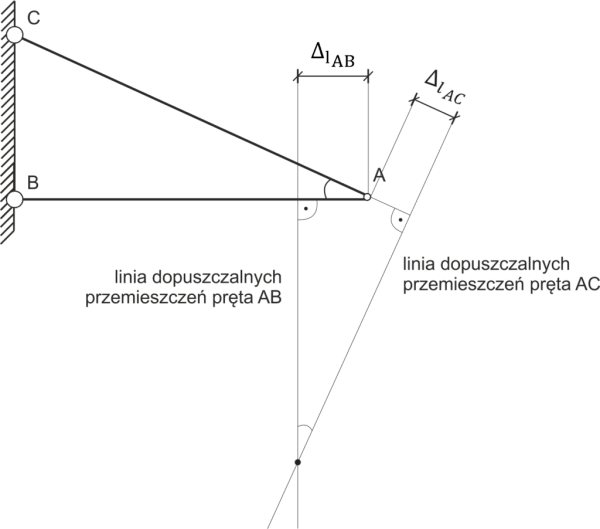
We notice the green triangle, describe two of its sides as a, b, and notice that it is similar to the small triangle a', b', \( \Delta l_{AB} \).
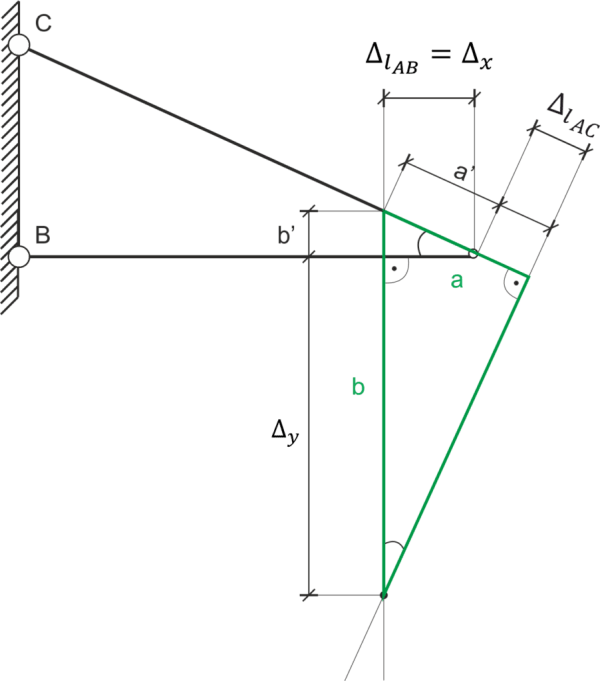
We calculate side a. \begin{aligned} &a=a' + |\Delta l_{AC}|\\ &|\Delta l_{AC}|=0.934 \ mm\\ &\frac{|\Delta l_{AB}|}{a'}=\cos30^{o}\\ &a'=\frac{0.409}{\frac{\sqrt3}{2}}=0.47 \ mm\\ &a=0.47 + 0.934 = 1.404 \ mm \end{aligned} We calculate side b. \begin{aligned} &b=b' + \Delta_{y}\\ &\frac{b'}{a'}=sin30^{o}\\ &b'=0.47\cdot 0.5 = 0.235 \ mm\\ &\frac{a}{b}=\sin30^{o}\\ &b=\frac{a}{sin30^{o}}=\frac{1.404}{0.5}\\ &b=2.808 \ mm\\ \end{aligned} We calculate the vertical and horizontal displacement of point A. \begin{aligned} &\Delta_{y}=b-b'\\ &\Delta_{y}=2.808 - 0.235 = 2.573 \ mm\\ &\Delta_{x}=\Delta l_{AB} = 1.438 \ mm\\ \end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
