Edupanda » Mechanika techniczna » Statics - Spatial force system » Reduction of a spatial arbitrary system of forces
List of examples
Example 1
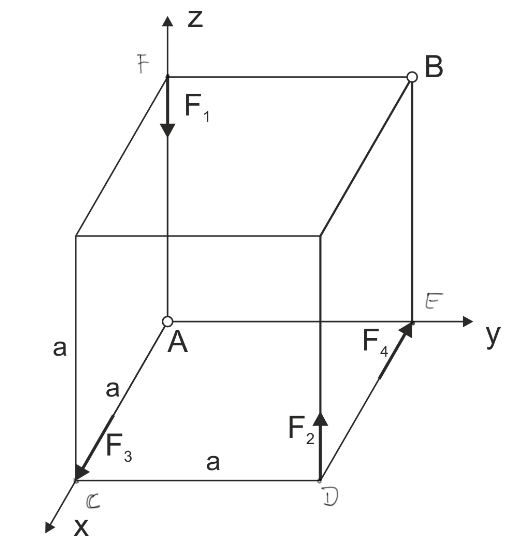
There is a spatial force system. a) Reduce the system at point A b) Reduce the system at point B c) Simplify the system to the simplest form. \begin{aligned} &F_{1}=2 \mathrm{kN} \\ &F_{2}=2 \mathrm{kN} \\ &F_{3}=2 \mathrm{kN} \\ &F_{4}=2 \mathrm{kN} \\ &a=1 \mathrm{~m} \end{aligned}
Example 2
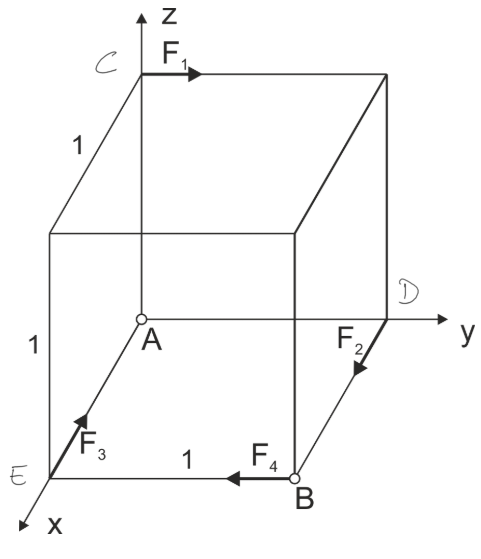
A spatial arrangement of forces is given. a) Reduce the arrangement at point A b) Reduce the arrangement at point B c) Reduce the arrangement to its simplest form. Draw the result of the reduction
\begin{aligned} &F_{1}=5 k N \\ &F_{2}=2 k N \\ &F_{3}=2 k N \\ &F_{4}=5 k N \end{aligned}Example 3
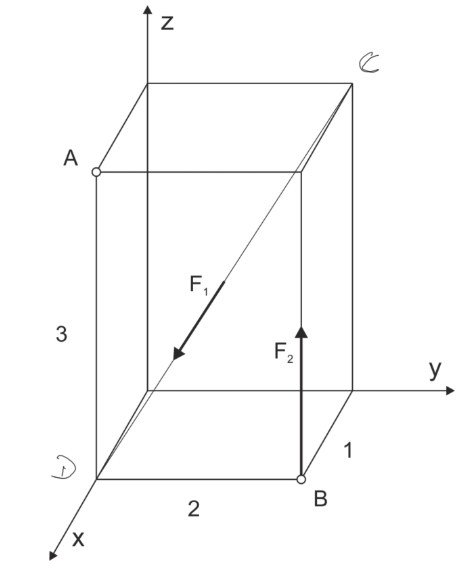
There is a spatial arrangement of forces. a) Simplify the arrangement at point A b) Simplify the arrangement at point B c) Simplify the arrangement to its simplest form.
\begin{aligned} &F_{1}=\sqrt{14} k N \\ &F_{2}=3 k N \end{aligned}Example 4
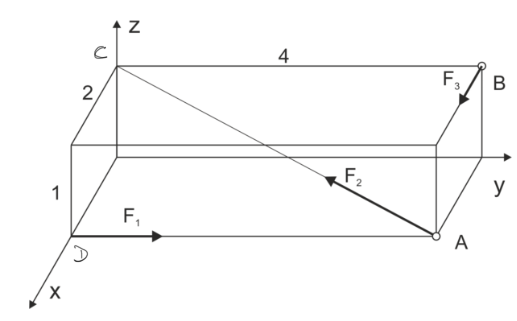
A spatial force system is given. a) Reduce the system at point A b) Reduce the system at point B c) Simplify the system to the simplest form.
\begin{aligned} &F_{1}=1 kN \\ &F_{2}=2 \sqrt{21} kN \\ &F_{3}=4 kN \end{aligned}Example 5
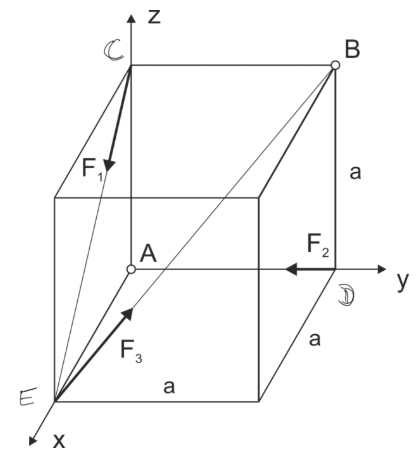
A spatial force system is given. a) Reduce the system at point A b) Reduce the system at point B c) Reduce the system to the simplest form.
\begin{aligned} &F_{1}=10 P \\ &F_{2}=\sqrt{2} P \\ &F_{3}=\sqrt{6} P \end{aligned}