Edupanda » Technical Mechanics » Statics - Planar force system » Equilibrium of a planar arbitrary system of forces I
List of examples
Example 1
A slanted bar is supported against a wall and connected with a hinge to a vertical bar, which is fixed. Release the system from constraints and write the equations of static equilibrium.
Example 2
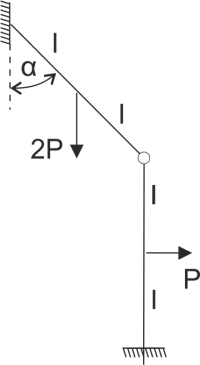
A configuration of three rods connected by hinges is given. The bottom rod is freely supported by a support. Release the system from constraints and write down the equations of static equilibrium.
Example 3
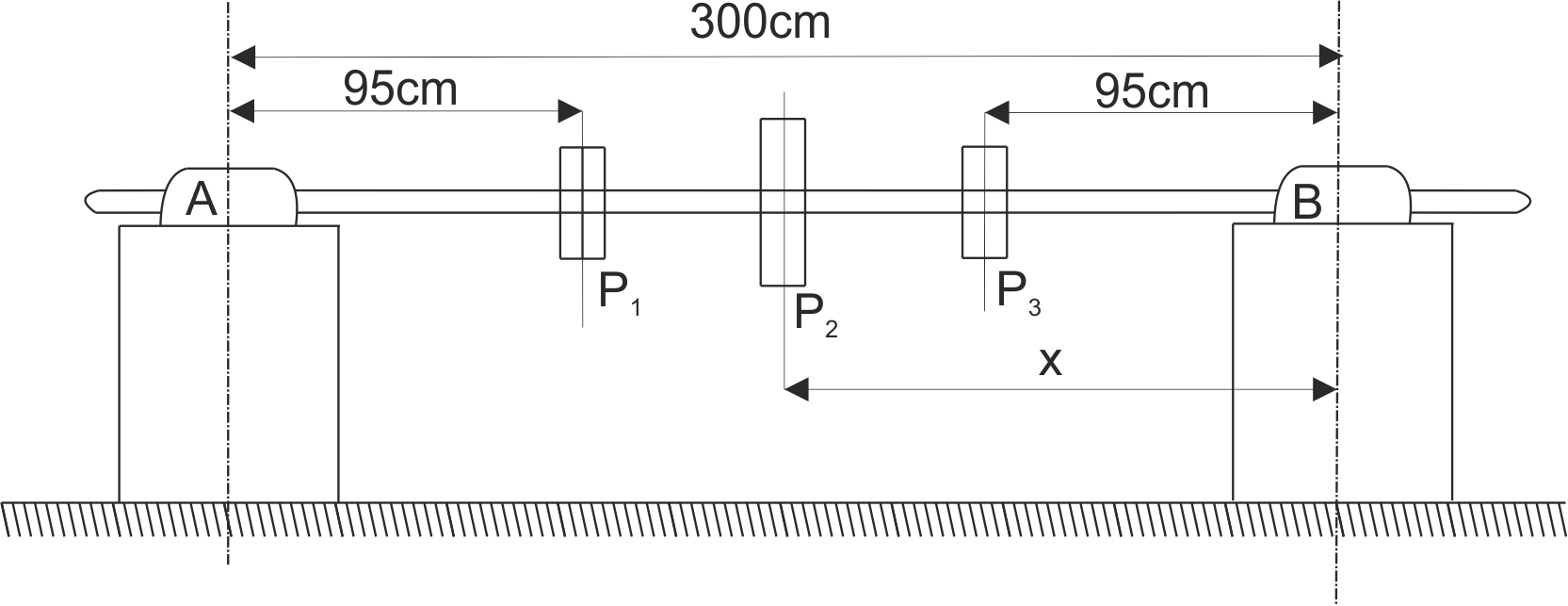
Transmission shaft AB has three pulleys with weights P1=3 kN, P2=5 kN, P3=2 kN. The dimensions are shown in the picture. At what distance x from bearing B should the wheel with weight P2 be mounted so that the reactions of both bearings are equal to each other? We disregard the weight of the shaft.
Example 4
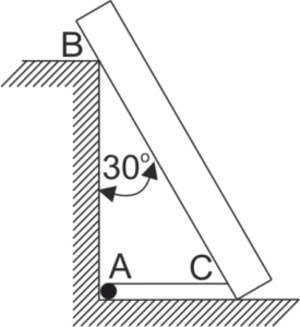
A uniform beam weighing 60 kg and measuring 4 m in length, resting on a smooth floor at one end and at point B – on a column measuring 3 m in height – forms a \(30^o\) angle with the vertical. The beam is held in this position by a rope AC pulled along the floor. Determine the tension in the rope T and the reactions at points B and C.
Example 5
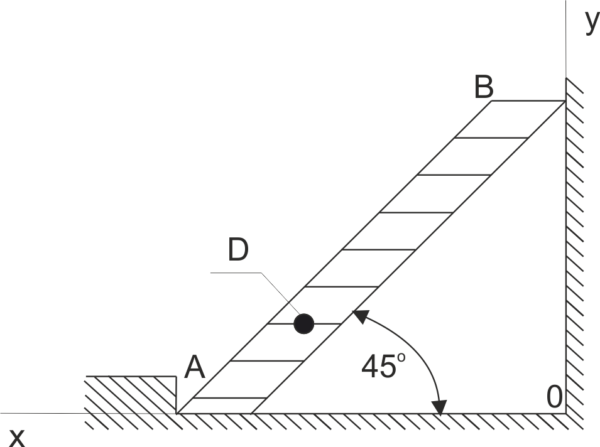
A ladder AB is resting against a smooth wall, inclined at an angle of 45^o to the horizontal. The mass of the ladder is 20 kg. At point D, which is 1/3 of the ladder's length away from the bottom end, there is a person with a mass of 60 kg. Determine the forces exerted by the ladder on support A and on the wall.
Example 6
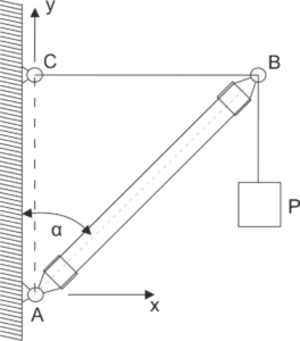
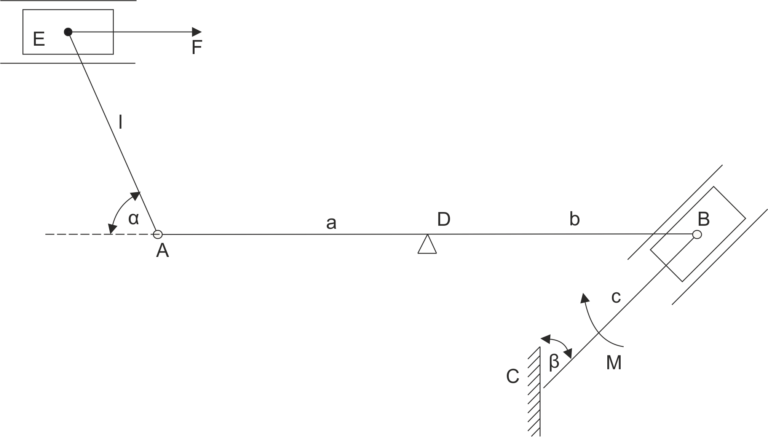
The crane consists of the beam AB, whose lower end is connected by a joint A to the wall, and the upper end is supported by a horizontal rope BC. Determine the tension T in rope BC and the vertical projection \(N_A\) of the support reaction at A, if the weight P is P=2 kN, the weight of the beam Q=1 kN is attached at the midpoint of AB, and the angle \( \alpha=45^o \).
Example 7
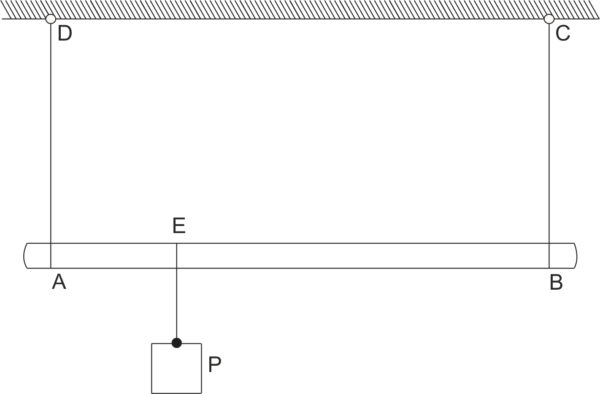
A homogeneous rod AB with a length of 1 m and weighing 20 N is suspended horizontally on two parallel ropes AC and BD. A weight P = 120 N is hung at point E on the rod, which is 0.25 m away from point A. Calculate the forces in the ropes \( T_{AC}, T_{BD} \).
Example 8
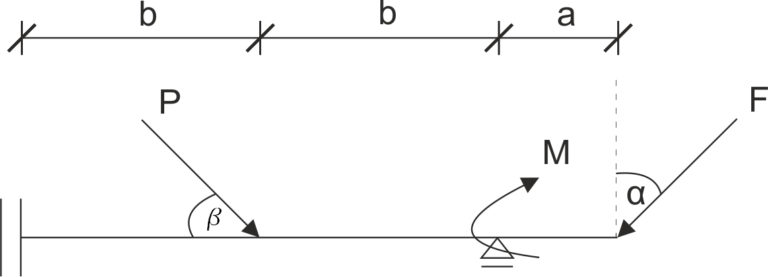
There is a beam supported by a vertical skate and a hinge sliding support. Release the system from restraints and write the equations for static equilibrium.
Example 9
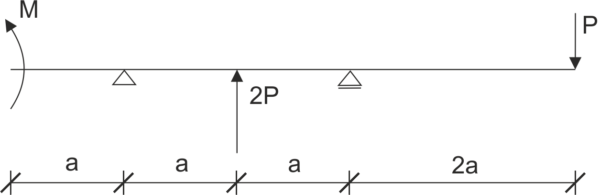
A beam is supported as shown in the diagram. Release the constraints and write the equilibrium equations.
Example 10
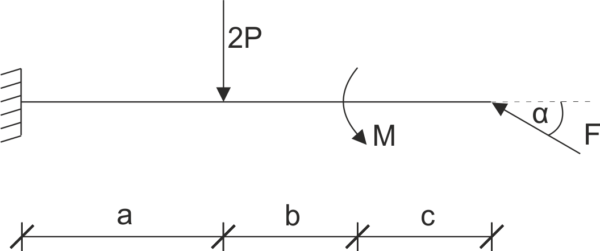
The beam is supported as shown in the figure. Release the system from constraints and write down the equilibrium equations.
Example 11
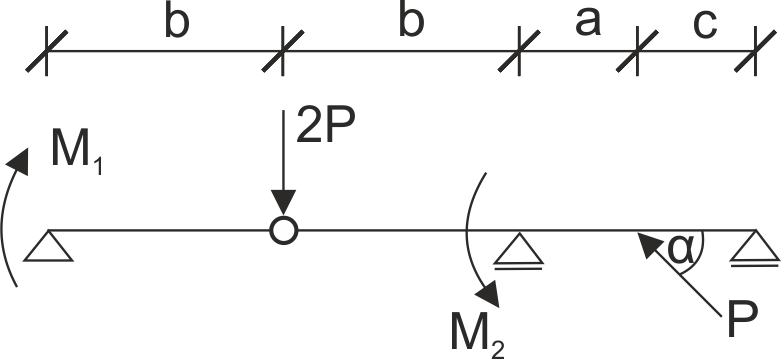
The beam is supported as shown in the drawing. Release the structure from the restraints, divide the hinged beam into simple beams, and write down the equations of equilibrium.
Example 12
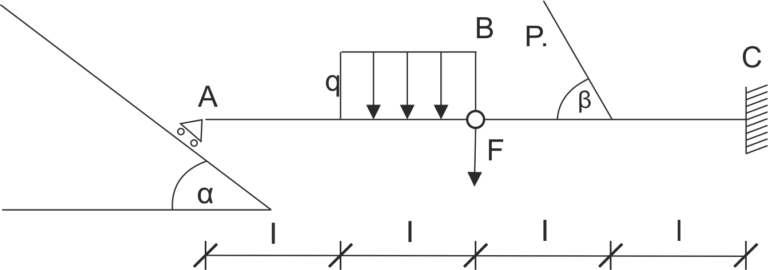
The beam shown in the picture is supported. Release the system from restraints, divide the hinged beam into straight beams, and write the equations of equilibrium.