Edupanda » Mechanika budowli » Method of displacements » Frames - thermal and geometrical loads
List of examples
Example 1
For the given frame, separately for each of the loads \(P, G, T\), determine the bending moment charts \(M_{\text{ost}}^P\), \(M_{\text{ost}}^G\), \(M_{\text{ost}}^T\).
Then add up the obtained charts to obtain \(M_{\text{ost}}^{P+G+T}\), based on which determine \(Q_{ost}^{P+G+T}\) and \(N_{ost}^{P+G+T}\).
Data:
\(
\alpha=10^{-5} \frac{1}{^o \mathrm{C}} \\
E J=2000 \mathrm{kNm}^2
\)
Example 2
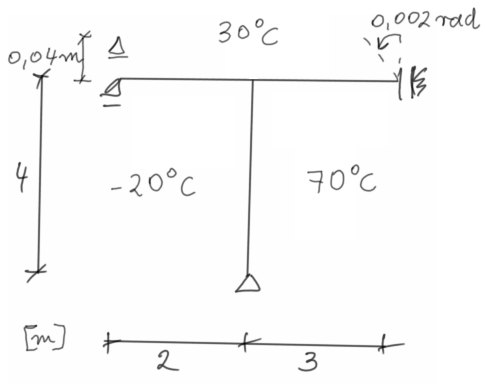
Draw the final moment charts separately for loads caused by support displacements, thermal loads due to uneven and uniform temperature.
Then, sum up the obtained charts and determine \(Q_{o s t}^{G+T}\) and \(N_{o s t}^{G+T}\) from the resulting chart.
Data:
\(
\alpha=10^{-5} \quad \text {thermal expansion coefficient} \\
\mathrm{EI}=2 \cdot 10^4 \mathrm{kNm}^2 \\
\mathrm{~h}:=0.2 \ m\\
\mathrm{t}_{\mathrm{m}}=10^o \mathrm{C}
\)
Example 4
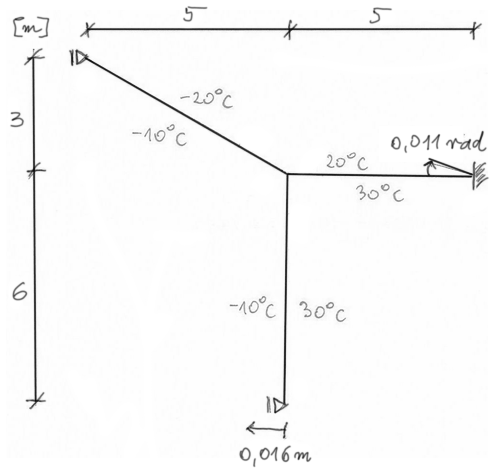
Draw separate charts of bending moments caused by loads resulting from support displacements, thermal loads from uniform and non-uniform temperature.
Then, sum up the charts of moments and based on this chart, create final charts of shear forces and normal forces.
Assume a rectangular section of 0.2x0.8m (w x h). Take E = 20 GPa, \( t_m = 10^o C \), \( \alpha = 1\cdot 10^{-5} \ \frac{1}{^o C} \).
Example 5
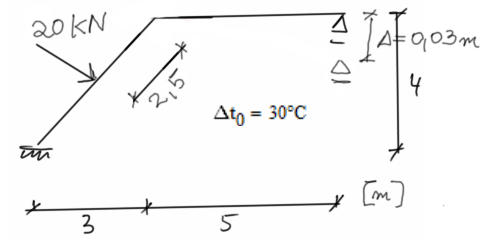
Draw separate bending moment diagrams for the loads caused by support displacements, uniform temperature variations, and non-uniform temperature variations.
Then sum up the moment diagrams.
Assume a bending stiffness of EI = 2000 kNm^2. Data: \(\Delta = 0.03 \ m\), E = 20 GPa, \(\Delta t_0 = 30^o C\), \(\alpha = 1 \cdot 10^{-5} \ \frac{1}{^o C}\).
Example 6
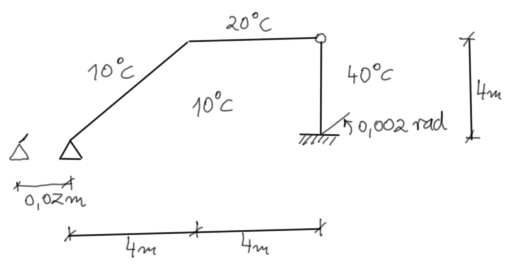
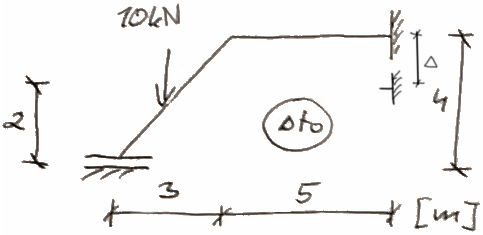
Draw separate charts for bending moments caused by loads, displacements of supports, and thermal effects from uniform and non-uniform temperature.
Then sum up the moment charts and based on this chart, create final charts for shear forces and normal forces.
Assume a bending stiffness of EI = 20,000 kNm^2. Assume h = 0.2 m, t_m = 5 degrees Celsius, and \(\alpha = 1 \cdot 10^{-5} \ \frac{1}{^o C} \).
Example 7
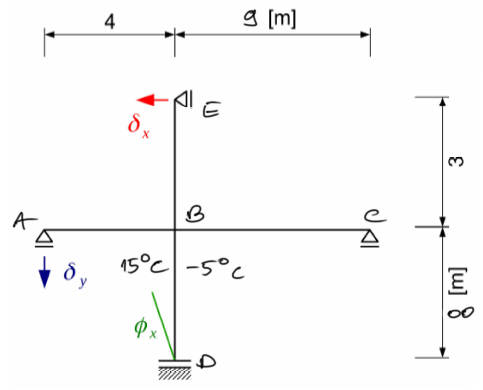
Draw separate charts for bending moments caused by loads, displacements of supports, uniform and non-uniform thermal effects. Then, add up the charts of moments and based on this chart, create final charts for shear forces and normal forces. Perform a global check. Data: E=205 GPa, section IPE220, \( t_m=40^o C \), \( \alpha = 1.2\cdot 10^{-6} \ \frac{1}{^o C} \), \( \delta x = 6 \ cm \), \( \delta y = 4 \ cm \), \( \phi x = 0.065 rad \).
Example 8
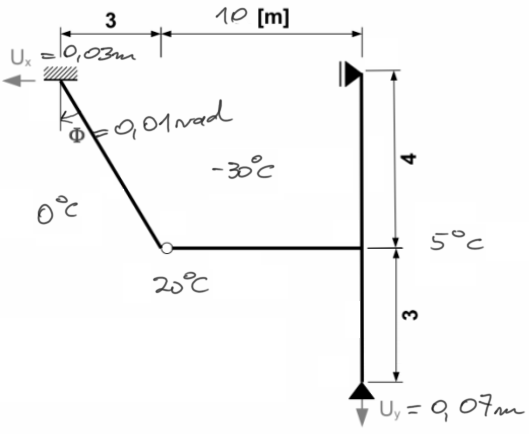
Draw charts of bending moments separately for the loads caused by support displacements, thermal effects from uniform and non-uniform temperature.
Then sum up the moment charts and based on this chart, create final charts of shear forces and normal forces.
Perform a global check.
Data: E=205 GPa, section IPE120, \( t_m=-15^o C \) (\( t_n=-15^o C \)), \( \alpha = 1.2\cdot 10^{-6} \ \frac{1}{^o C} \), \( U_x = 3 \ cm \), \( U_y = 7 \ cm \), \( \phi = 0.01 rad \).
