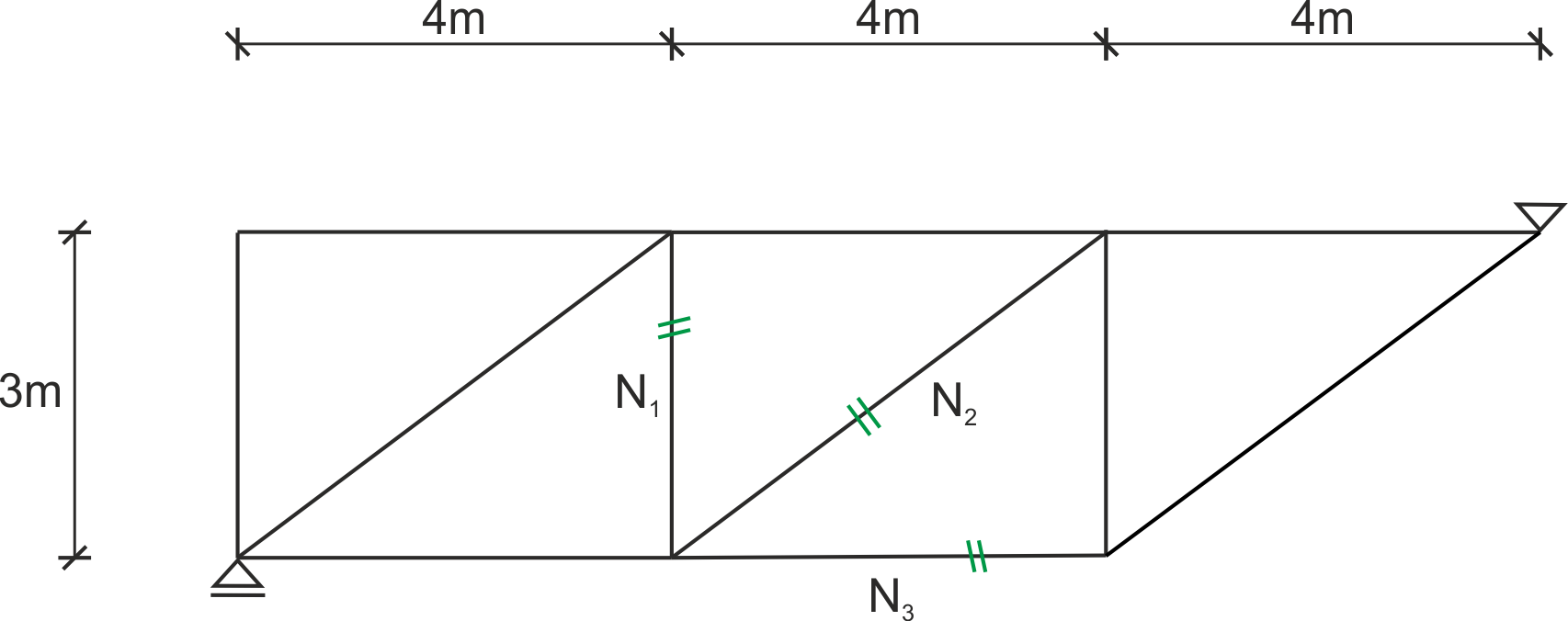
Solution
To calculate the influence lines for the selected bars, you can use either the method of node equilibrium or, preferably, the Ritter method.

We write the equations of static equilibrium:
\begin{aligned} &\sum M_{B}=0 \\ &V_{A} \cdot 12-1 \cdot(12-x)=0 \\ &V_{A}=\frac{12-x}{12} \\ &\sum y=0 \\ &V_{A}-1+V_{B}=0 \\ &V_{B}=\frac{12}{12}-\frac{12-x}{12}=\frac{x}{12} \end{aligned}We draw an auxiliary diagram for the Beta section and write the equations of equilibrium needed to calculate the desired forces. Note - we consider two cases: when the force has not yet arrived and when we already see the force from that side of the truss. The case when the force is in the bar through which the Ritter cut was made is usually omitted, and that part is represented by a dashed line on the graph - although different approaches to this issue can be found in the literature.
Beta section
 \begin{aligned}
&\text { Interval }-I x \in(0 ; 4) \\
&\sum Y=0 \\
&N_{1}+V_{B}=0 \\
&N_{1}=-V_{B} \\
&N_{1}=-\frac{x}{12} \\
&N_{1}(0)=0\\
&N_{1}(4)=-1 / 3
\end{aligned}
\begin{aligned}
&\text { Interval }-I x \in(0 ; 4) \\
&\sum Y=0 \\
&N_{1}+V_{B}=0 \\
&N_{1}=-V_{B} \\
&N_{1}=-\frac{x}{12} \\
&N_{1}(0)=0\\
&N_{1}(4)=-1 / 3
\end{aligned}
 \begin{aligned}
&\text { Interval-II } x \in(8 ; 12) \\
&\sum Y=0 \\
&N_{1}+V_{B}-1=0 \\
&N_{1}=1-V_{B} \\
&N_{1}=\frac{12}{12}-\frac{x}{12}=\frac{12-x}{12} \\
&N_{1}(8)=1 / 3\\
&N_{1}(12)=0
\end{aligned}
\begin{aligned}
&\text { Interval-II } x \in(8 ; 12) \\
&\sum Y=0 \\
&N_{1}+V_{B}-1=0 \\
&N_{1}=1-V_{B} \\
&N_{1}=\frac{12}{12}-\frac{x}{12}=\frac{12-x}{12} \\
&N_{1}(8)=1 / 3\\
&N_{1}(12)=0
\end{aligned}
We draw an auxiliary diagram for the Alpha section and proceed as before.
 \begin{aligned}
&\text { Section - } \alpha \\
&\text { Interval - I } x \in(0 ; 4) \\
&\sin \alpha=0.8 \\
&\cos \alpha=0.6
\end{aligned}
\begin{aligned}
&\sum Y=0 \\
&-N_{2} \cdot \cos \alpha+V_{B}=0 \\
&N_{2}=\frac{V_{B}}{0.6} \\
&N_{2}=\frac{x}{7.2} \\
&N_{2}(0)=0\\
&N_{2}(4)=0.555
\end{aligned}
\begin{aligned}
&\sum M_{R}=0 \\
&N_{3} \cdot 3-V_{B} \cdot 4=0 \\
&N_{3}=\frac{4}{3} \frac{x}{12}=\frac{x}{9} \\
&N_{3}(0)=0\\
&N_{3}(4)=0.444
\end{aligned}
\begin{aligned}
&\text { Section - } \alpha \\
&\text { Interval - I } x \in(0 ; 4) \\
&\sin \alpha=0.8 \\
&\cos \alpha=0.6
\end{aligned}
\begin{aligned}
&\sum Y=0 \\
&-N_{2} \cdot \cos \alpha+V_{B}=0 \\
&N_{2}=\frac{V_{B}}{0.6} \\
&N_{2}=\frac{x}{7.2} \\
&N_{2}(0)=0\\
&N_{2}(4)=0.555
\end{aligned}
\begin{aligned}
&\sum M_{R}=0 \\
&N_{3} \cdot 3-V_{B} \cdot 4=0 \\
&N_{3}=\frac{4}{3} \frac{x}{12}=\frac{x}{9} \\
&N_{3}(0)=0\\
&N_{3}(4)=0.444
\end{aligned}
 Interval $-II x \in(8 ; 12)$
\begin{aligned}
&\sin \alpha=0.8 \\
&\cos \alpha=0.6
\end{aligned}
\begin{aligned}
&\sum Y=0 \\
&-N_{2} \cdot \cos \alpha+V_{B}-1=0 \\
&N_{2}=\frac{x-12}{7.2} \\
&N_{2}(8)=-0.555\\
&N_{2}(12)=0
\end{aligned}
\begin{aligned}
&\sum M_{R}=0 \\
&N_{3} \cdot 3-V_{B} \cdot 4+1 \cdot(x-8)=0 \\
&N_{3}=\frac{4}{3} \frac{x}{12}-\frac{3(x-8)}{3 \cdot 3}=\frac{x-3 x+24}{9}=\frac{24-2 x}{9} \\
&N_{3}(8)=0.888\\
&N_{3}(12)=0
\end{aligned}
Interval $-II x \in(8 ; 12)$
\begin{aligned}
&\sin \alpha=0.8 \\
&\cos \alpha=0.6
\end{aligned}
\begin{aligned}
&\sum Y=0 \\
&-N_{2} \cdot \cos \alpha+V_{B}-1=0 \\
&N_{2}=\frac{x-12}{7.2} \\
&N_{2}(8)=-0.555\\
&N_{2}(12)=0
\end{aligned}
\begin{aligned}
&\sum M_{R}=0 \\
&N_{3} \cdot 3-V_{B} \cdot 4+1 \cdot(x-8)=0 \\
&N_{3}=\frac{4}{3} \frac{x}{12}-\frac{3(x-8)}{3 \cdot 3}=\frac{x-3 x+24}{9}=\frac{24-2 x}{9} \\
&N_{3}(8)=0.888\\
&N_{3}(12)=0
\end{aligned}
Graphs