Lista zadań
Przykład 1

Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 2

Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 3
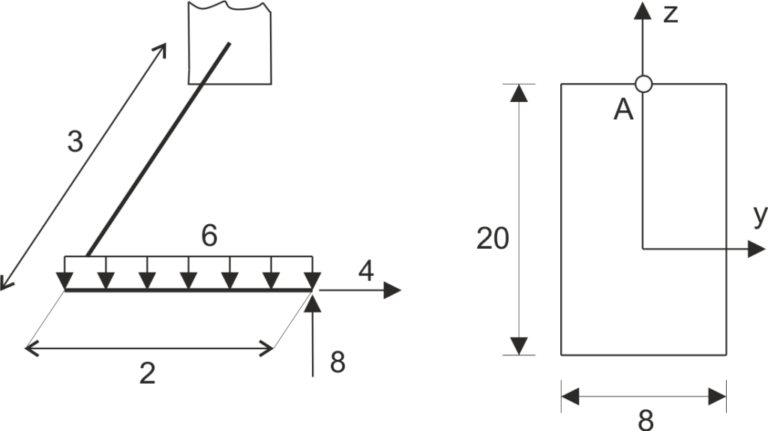
Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 4

Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 5
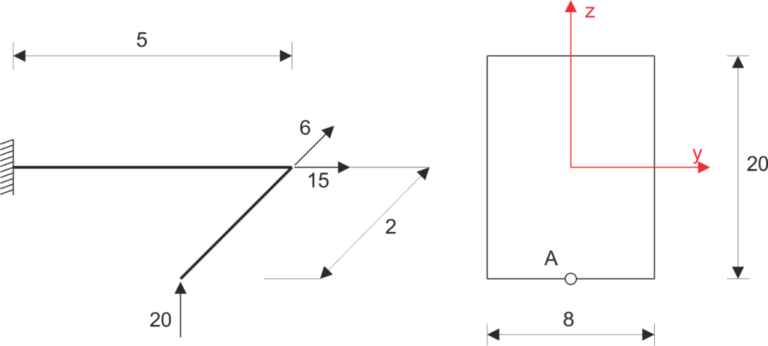
Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 6

Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 7

Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A przekroju utwierdzenia konstrukcji o schemacie jak na rysunku.
Przykład 8

Wyznaczyć naprężenia zredukowane według hipotezy Hubera-Misesa-Hencky’ego w punkcie A oraz B przekroju utwierdzenia konstrukcji o schemacie jak na rysunku. Podaj stosunek naprężeń zredukowanych w tych punktach.
Przykład 9
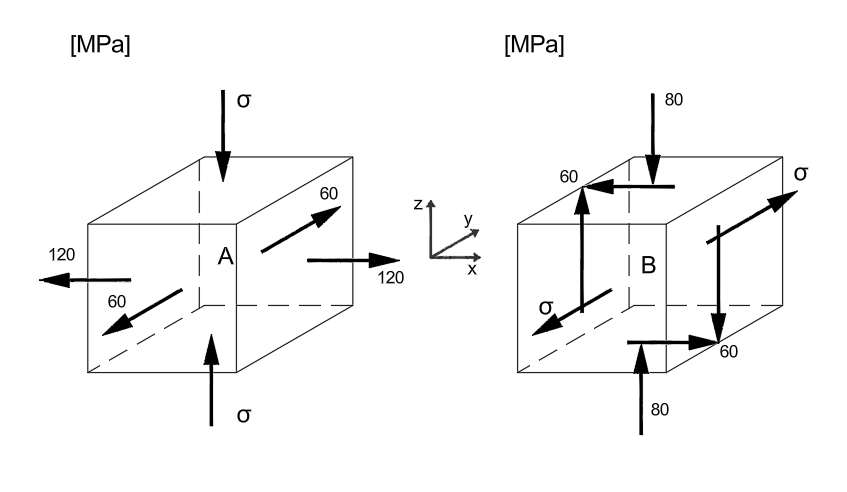
Wyznaczone zostały naprężenia w dwóch różnych punktach konstrukcji. Wartości, kierunki i zwroty tych naprężeń zostały schematycznie przedstawione niżej na rysunku.
Korzystając z hipotezy Coulomba-Treski, przyjmując wartość graniczną naprężeń równą granicy plastyczności:
\[ R_{pl} = 180 + 20x \ \text{[MPa]} \]wyznaczyć w jakich granicach może się zmieniać wartość \(\sigma\) (bez zmiany zwrotu), aby podane stany były bezpieczne.