Zginanie ukośne - wstęp
Zginanie ukośne to rodzaj zginania, w którym kierunek wektora momentu gnącego nie pokrywa się z żadną z głównych osi bezwładności przekroju. Oznacza to, że płaszczyzna działania obciążenia nie jest równoległa do żadnej z tych osi. Rzutując wektor momentu gnącego na główne centralne osie układu, otrzymujemy składowe momentu (M) w osiach (y) i (z).
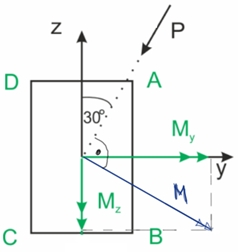
Rys1. Zginanie ukośne - rzutowanie momentu na osie główne centralne
Z tego kursu dowiesz się
- jak wyznaczyć reakcje i narysować wykresy sił wewnętrznych,- jak narysować rozkład naprężeń normalnych,
- jak wyznaczyć bryłę naprężeń,
- jak wyznaczyć i narysować położenie osi obojętnej,
- jak zwymiarować belkę zginaną ukośnie z warunku wytrzymałości,
- jak wyznaczyć dopuszczalną wartość obciążenia mając dany konkretny przekrój,
W ogólności oś obojętna nie pokrywa się z linią działania wektora momentu gnącego, choć przechodzi przez środek ciężkości przekroju. Oś obojętna zginania to miejsce geometryczne punktów, dla których naprężenia są równe zero.
Równanie naprężenia normalnego uwzględniające działanie momentu zginającego w kierunku dwóch osi głównych centralnych:
$$\sigma(x) = \frac{-M_y}{I_y} \cdot z - \frac{M_z}{I_z} \cdot y$$
gdzie:
- \( \sigma \) to naprężenie normalne,
- \( M_y, M_z \) to momenty zginające,
- \( y, z \) to odległości od środka ciężkości po osiach głównych centralnych do punktu przekroju w którym chcemy obliczyć naprężenia,
- \( I_y, I_z \) to główne centralne momenty bezwładności przekroju poprzecznego.
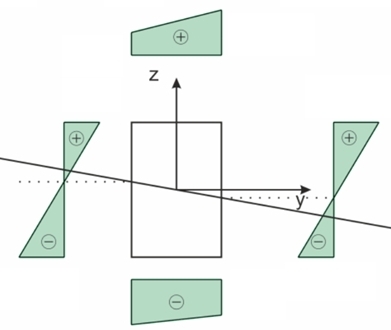
Rys2. Przykładowy wykres naprężeń normalnych - zginanie ukośne
Do dyspozycji masz kursy wideo oraz szeroką bazę zadań z rozwiązaniami dla każdego rodzaju zginania osobno.
ZOBACZ TEŻ

