Z tego kursu dowiesz się:
- jak wyznaczać reakcje podporowe w ramach,
- jak sprawdzić poprawność obliczonych reakcji,
- jak rysować wykresy sił normalnych, tnących i momentów zginających w ramach prostych, skośnych i przegubowych,
- jak sprawdzić równowagę węzła (sprawdzenie poprawności wykresów),
- wykresy nauczysz się rysować dwiema metodami - z zapisywaniem funkcji sił wewnętrznych oraz bez zapisywania tych funkcji,

to wszystko zaczynając od bardzo prostych przykładów ram, przechodząc do ram z większą ilością i różnorodnością obciążeń, kończąc na ramach z prętami skośnymi zarówno z przegubem, jak i bez przegubu.

Siły wewnętrzne w ramach

W dziedzinie wytrzymałości materiałów, zrozumienie sił wewnętrznych jest kluczowym elementem dla projektowania i analizy konstrukcji. Siły wewnętrzne, takie jak siła normalna, siła tnąca i moment zginający, stanowią fundamentalne wartości, które kształtują zachowanie się materiałów pod obciążeniem.

Podobnie jak w belkach, w ramach również działają te same siły wewnętrzne, wpływając na ich wytrzymałość i stabilność. Analiza tych sił pozwala inżynierom lepiej zrozumieć zachowanie się ram pod różnymi warunkami obciążenia oraz odpowiednio je zaprojektować.


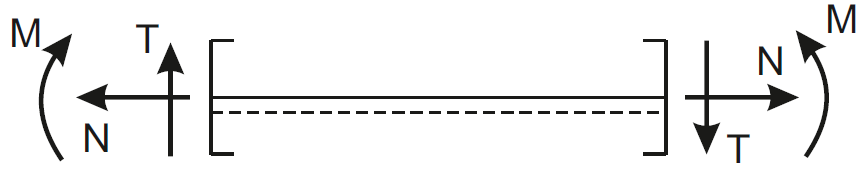
Rys1. Konwencja znakowania sił wewnętrznych


Ramy są niezwykle wszechstronne i znajdują zastosowanie w wielu różnych typach konstrukcji, od budynków mieszkalnych i komercyjnych po mosty, hale sportowe i elementy infrastruktury. Ich zastosowanie pozwala na tworzenie trwałych, stabilnych i estetycznych struktur, które mogą wytrzymać różnorodne obciążenia i warunki środowiskowe.

Trudności obliczeniowe

Z punktu widzenia obliczeń sił wewnętrznych obliczanie ram jest trochę trudniejsze od obliczania belek.

Po pierwsze jak już nauczymy się korzystać z konwencji znakowania idąc od lewej lub od prawej strony belki to pojawia się na początku problem z interpretacją znakowania dla pręta pionowego.
Chyba najprościej na początku narysować sobie na konwencji znakowania tzw. "spody", to znaczy umowny dół pręta. Jeśli rozwiązując ramę na pręcie pionowym też sobie zaznaczymy spody (po dowolnej stronie) to prościej nam będzie skorzystać ze znakowania. Zawsze możemy obrócić sobie kartkę tak żeby patrzeć na pręt pionowy tak jak na poziomą belkę - zakładam że obliczanie belek już mamy opanowanie.

Kolejny problem pojawi się również jeśli będziemy mieli pręt skośny, ponieważ do tej pory dla pręta poziomego (dla belki) jeśli siła działała osiowo (poziomo) to była siłą normalną, jeśli działała poprzecznie do belki (pionowo), to była siłą tnącą.
Dla pręta pionowego z kolei siły pionowe to były siły osiowe, poziome to były tnące do pręta.
Dla pręta skośnego - jeśli obciążymy go siłą poziomą, to tą siłę musimy zrzutować na kierunek w osi pręta (składowa normalna do pręta) i na kierunek prostopadle do osi pręta (składowa tnąca). No i tu dochodzi kolejna umiejętność którą się musimy wykazać żeby poprawnie narysować wykresy - rzutowanie sił na składowe.

Fajnym sprawdzeniem poprawności narysowanych wykresów sił wewnętrznych jest sprawdzenie równowagi węzła które pokażemy na poniższym przykładzie.

Kurs wideo pokazujący jak narysować wykresy sił wewnętrznych
dla ramy przegubowej z prętem skośnym zapisując funkcje sił wew.

Poniżej rozwiązanie z opisaniem rzutowania sił na składowe dla pręta skośnego oraz sprawdzeniem na końcu równowagi węzła

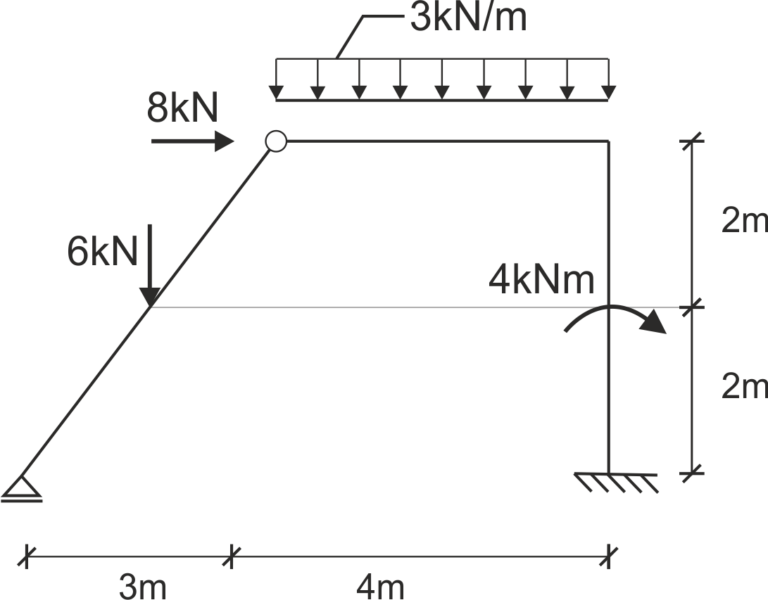
Temat ramy skośnej

Rozwiązanie

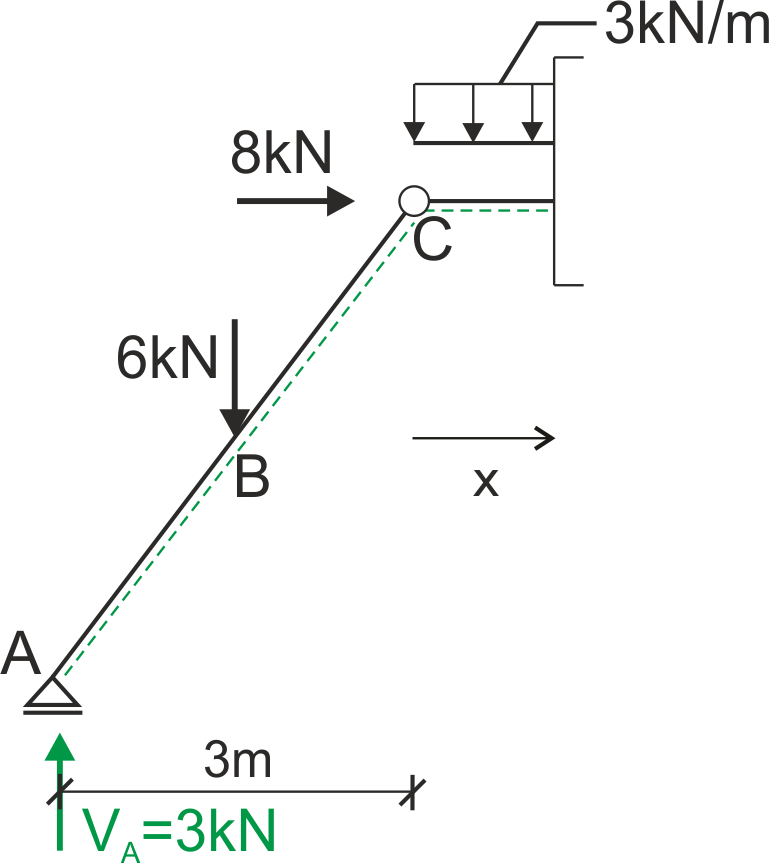
1) Zaznaczenie spodów, opisanie punktów charakterystycznych, naniesienie reakcji w podporach i ich obliczenie
Tak jak wspominaliśmy we wstępie - zaznaczamy sobie spody na ramie.
Dla porządku podpisujemy punkty charakterystyczne i koniecznie zaznaczamy reakcje - będziemy przystępowali do ich obliczenia.

Równania równowagi statycznej

\begin{aligned} &\sum M_{C}^L = 0\\ &-6 \cdot \frac{3}{2} + V_{A} \cdot 3 = 0\\ &V_{A} = \frac{6 \cdot \frac{3}{2}}{3} = 3 \, \text{kN}\\ \end{aligned} \( \quad \quad \) \begin{aligned} &\Sigma X = 0\\ &8 + H_{F} = 0\\ &H_{F} = -8 \, \text{kN}\\ \end{aligned}
\begin{aligned} &\Sigma Y = 0\\ &V_{A} - 6 - 3 \cdot 4 + V_{F} = 0\\ &V_{F} = -\left(V_{A} - 6 - 3 \cdot 4\right) = 15 \, \text{kN}\\ \\ &\Sigma M_{A} = 0\\ &6 \cdot \frac{3}{2} + 8 \cdot 4 + 3 \cdot 4 \cdot 5 + 4 - V_{F} \cdot 7 + M_{F} = 0\\ &M_{F} = -\left(6 \cdot \frac{3}{2} + 8 \cdot 4 + 3 \cdot 4 \cdot 5 + 4 - V_{F} \cdot 7\right) = 0 \, \text{kNm} \end{aligned}
2) Obliczenie sił wewnętrznych
Mając obliczone reakcje przechodzimy do liczenia sił wewnętrznych. Pokażemy tutaj jak dla pręta skośnego zrzutować siłę na kierunek normalny i tnący do pręta.

Rzutowanie reakcji VA na kierunek normalny i tnący do pręta
Dobrym pomysłem jest zrobić taki rysunek na którym zaznaczymy kierunek pionowy, poziomy, oś pręta (kierunek normalny) i prostopadłą do osi pręta (kierunek tnący).
Kąt alfa przyjmuję patrząc na ramę między poziomem i osią pręta.
Dodatkowo można sobie zaznaczyć zwrot dodatniej siły normalnej i dodatniej siły tnącej, który obowiązuje analizując pręt skośny od strony punktu A.

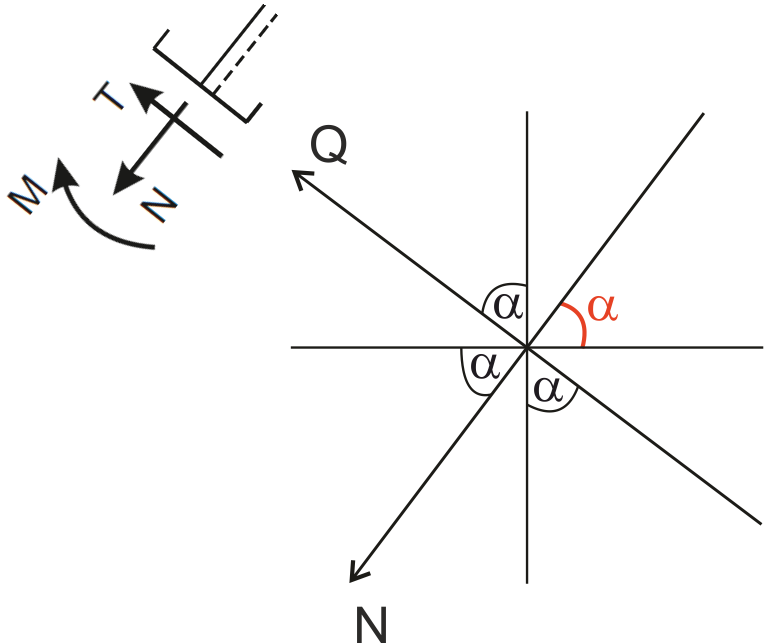
Na takim rysunku co drugi kąt to będzie kąt alfa.

Teraz jak chcę zrzutować reakcję \( V_A=3 \ kN \) na kierunek normalny i tnący do pręta to rysuję sobie ją na tej "pajęczynie" u góry.
Dwie najbliższe składowe to normalna i tnąca, a co najważniejsze do zapamiętania, to to, że: ta składowa przy której jest kąt alfa jest mnożona razy cosinus tego kąta, a druga składowa razy sinus alfa.
Zobacz na rysunek poniżej.


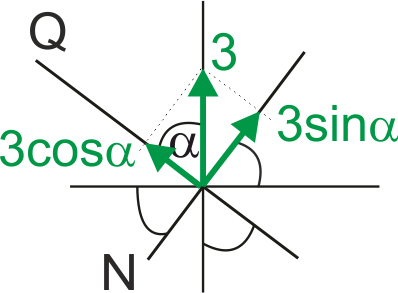
No to w zasadzie wszystko wiemy, rozpisujemy funkcje sił wewnętrznych we wszystkich przedziałach:

Przedział AB \( 0 \leq x \leq 1.5\)

 \( \quad \quad \)
\begin{aligned} &Q(x) = 3 \cos (\alpha) = 1.8 \, \text{kN} \\ &M(x) = 3x \\ &M(0) = 0 \\ &M(1.5) = 4.5 \, \text{kNm} \\ &N(x) = 3 \sin (\alpha) = -2.4 \, \text{kN} \end{aligned}

Przedział BC \( 1.5 \leq x \leq 3\)

 \( \quad \quad \)
\begin{aligned} &Q(x) = 3 \cos (\alpha) - 6 \cos (\alpha) = -1.8 \, \text{kN} \\ &M(x) = 3x - 6 \cdot(x - 1.5) \\ &M(1.5) = 4.5 \, \text{kNm} \\ &M(3) = 0 \\ &N(x) = 3 \sin (\alpha) + 6 \sin (\alpha) = -2.4 \, \text{kN} \end{aligned}

Przedział CD \( 0 \leq x \leq 4\)

 \( \quad \quad \)
\begin{aligned} & \mathrm{N}(\mathrm{x})=-8 \ \mathrm{kN} \\ & \mathrm{Q}(\mathrm{x})=3-6-3 \cdot \mathrm{x}=-3 \cdot \mathrm{x}-3 \\ & \mathrm{Q}(0)=-3 \ \mathrm{kN} \\ & \mathrm{Q}(4)=-15 \ \mathrm{kN} \\ & \mathrm{M}(\mathrm{x})=3 \cdot(3+\mathrm{x})-6 \cdot(1.5+\mathrm{x})-3 \cdot \mathrm{x} \cdot \frac{\mathrm{x}}{2} \\ & \mathrm{M}(0)=0 \ \mathrm{kNm} \\ & \mathrm{M}(4)=-36 \ \mathrm{kNm} \end{aligned}

Przedział FE \( 0 \leq x \leq 2\)

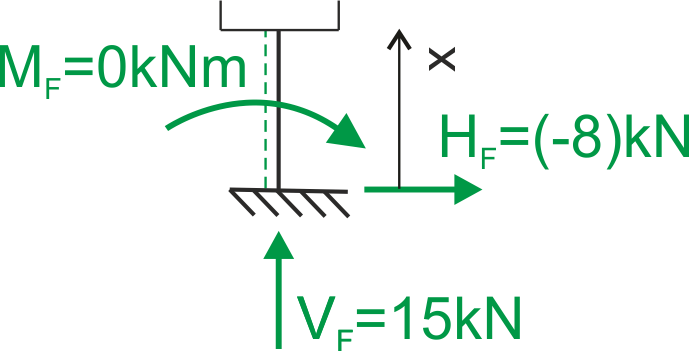
 \( \quad \quad \)
\begin{aligned} & \mathrm{N}(\mathrm{x})=-15 \ \mathrm{kN} \\ & \mathrm{Q}(\mathrm{x})=8 \ \mathrm{kN} \\ & \mathrm{M}(\mathrm{x})=-8 \cdot \mathrm{x} \\ & \mathrm{M}(0)=0 \\ & \mathrm{M}(2)=-16 \ \mathrm{kNm} \end{aligned}

Przedział ED \( 2 \leq x \leq 4\)

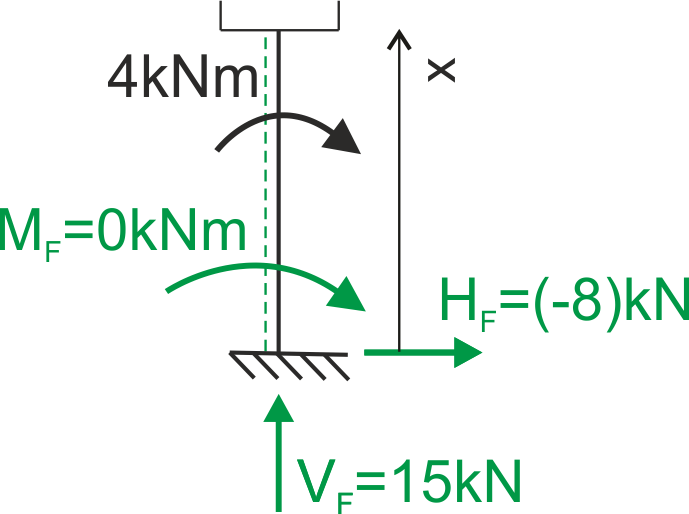
 \( \quad \quad \)
\begin{aligned} & \mathrm{N}(\mathrm{x})=-15 \ \mathrm{kN} \\ & \mathrm{Q}(\mathrm{x})=8 \ \mathrm{kN} \\ & \mathrm{M}(\mathrm{x})=-8 \cdot \mathrm{x}-4 \\ & \mathrm{M}(2)=-20 \ \mathrm{kNm} \\ & \mathrm{M}(4)=-36 \ \mathrm{kNm} \end{aligned}

Na podstawie obliczonych wartości sił wewnętrznych rysujemy wykresy
3) Wykresy sił wewnętrznych




4) Sprawdzenie równowagi węzła
To jak sprawdzić równowagę węzła pokazujemy w osobnym wstępie teoretycznym - ZOBACZ TUTAJ.
Poniżej znajdziesz również odnośniki do licznych przykładów rozwiązania zarówno ram prostych jak i z prętem/prętami skośnymi, a także ramy w przegubami.