Jak sprawdzić równowagę węzła w ramie
Jak sprawdzić równowagę węzła w ramie?
Węzeł jest to punkt ramy w którym łączą się dwa lub więcej prętów. Mając narysowane wykresy sił wewnętrznych dla ramy możemy ocenić ich poprawność poprzez wykonanie sprawdzenia równowagi węzła.Polega ono na tym, że odczytujemy z wykresów wartości i zwroty siły normalnej, siły tnącej i momentu gnącego z każdej strony węzła i sprawdzamy czy dla tak odczytanych sił wewnętrznych spełnione są równania równowagi statycznej - suma rzutów sił na oś x, y oraz suma momentów ma być równa zero.
Pierwszą rzeczą którą musimy zrobić jest poprawne odczytanie sił z wykresów, musimy pamiętać o konwencji znakowania:
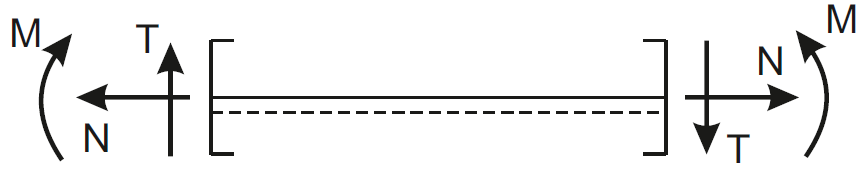
Rys1. Konwencja znakowania sił wewnętrznych
Następnie jeśli do węzła schodzi jakiś pręt skośny, musimy umieć rzutować siły pod kątem na składowe poziome i pionowe.
Przykład z prętem skośnym pokażemy później, a teraz zobaczmy jak będzie wyglądało sprawdzenie równowagi węzła dla ramy prostokątnej.
Żeby sprawdzić równowagę węzła oczywiście musimy mieć narysowane wykresy sił wewnętrznych, nie będziemy przechodzili przez rysowanie wykresów, jeśli chcesz przećwiczyć to zagadnienie, to zapoznaj się ze wstępem dotyczącym sił wewnętrznych w ramach.
Poniżej odnośniki do bazy zadań, a pod nimi dwa przykłady równowagi węzła.
Przykład 1
Równowaga węzła prostokątnego
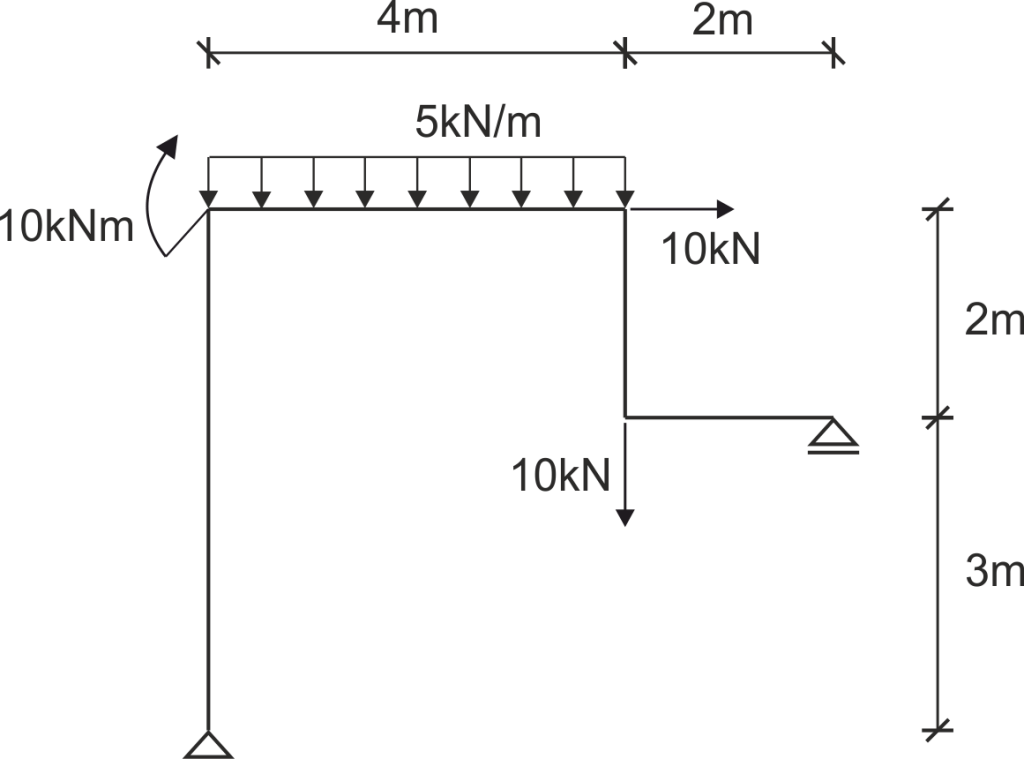
Rys2. Temat - przykład 1
Dla tego przykładu narysowano wykresy sił wewnętrznych jak poniżej:
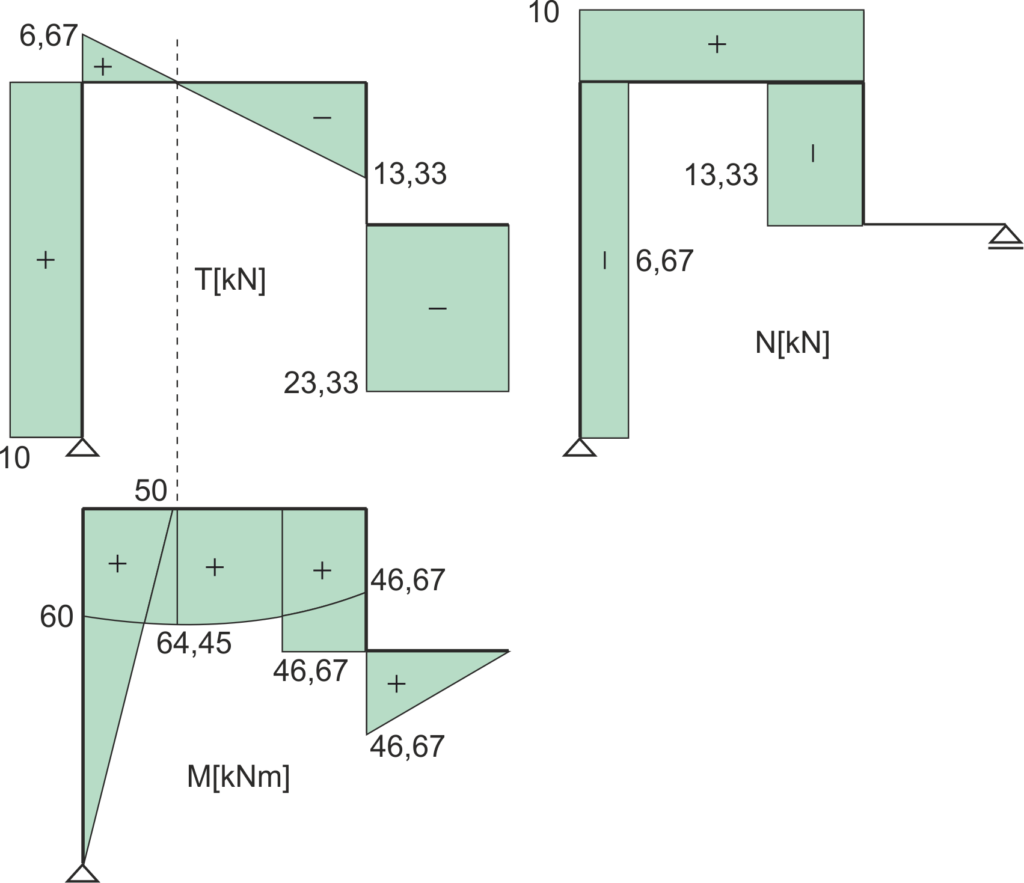
Rys3. Przykład 1 - wykresy sił wewnętrznych
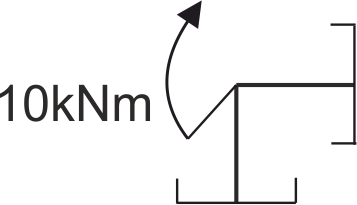
Rys4. Wycięcie pierwszego węzła do równowagi
Z prawej strony tego węzła patrząc na wykresy mamy siły: tnąca +6,67kN, normalna +10kN, moment gnący +60kNm.
Patrzymy na konwencję znakowania, widok z prawej strony - tam są zaznaczone zwroty dodatnich sił wewnętrznych, na analizowanym wykresie wszystkie siły są dodatnie, więc mają takie zwroty jak na konwencji znakowania powyżej (widok z prawej strony).
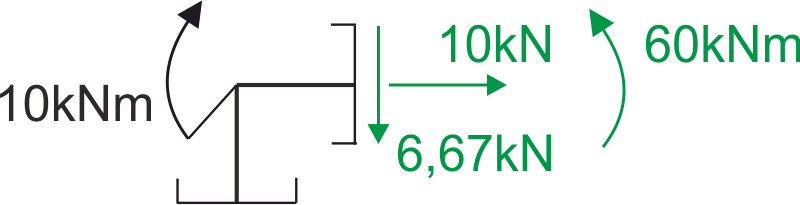
Rys5. Węzeł pierwszy - zaznaczenie sił przekrojowych od prawej strony
Przyjmijmy spody po prawej stronie pręta pionowego - i teraz mamy dwie możliwości - albo obracamy pręt pionowy tak, żeby mieć spody na dole, wtedy mamy taki przekrój wycinając węzeł, że patrzymy od lewej strony.
Albo obracamy konwencję znakowania spodami do przyjętych spodów (czyli przeciwnie do ruchu wskazówek zegara o 90 stopni) - i tą wersję pokażę poniżej.
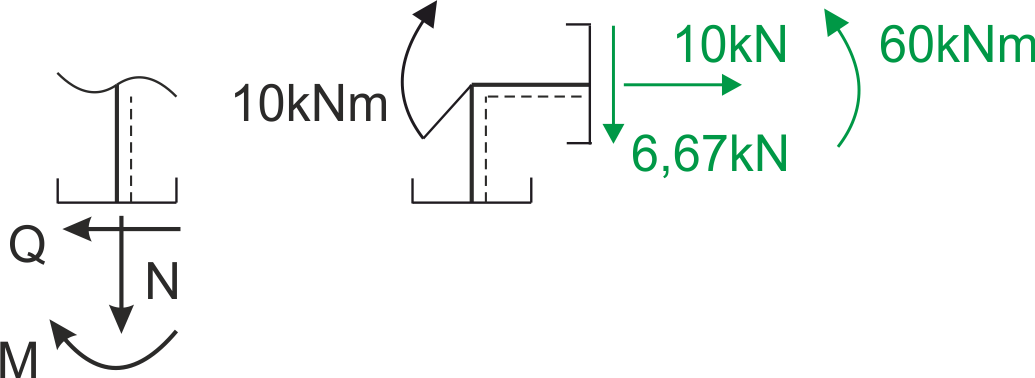
Rys6. Obrócenie i dopasowanie spodów dla pręta pionowego
Zaznaczamy więc te siły pod przekrojem z odpowiednimi zwrotami, dla siły normalnej, która jest ujemna zwrot jest przeciwny niż na konwencji znakowania, a dla siły tnącej i momentu gnącego zwroty są zgodne z konwencją.
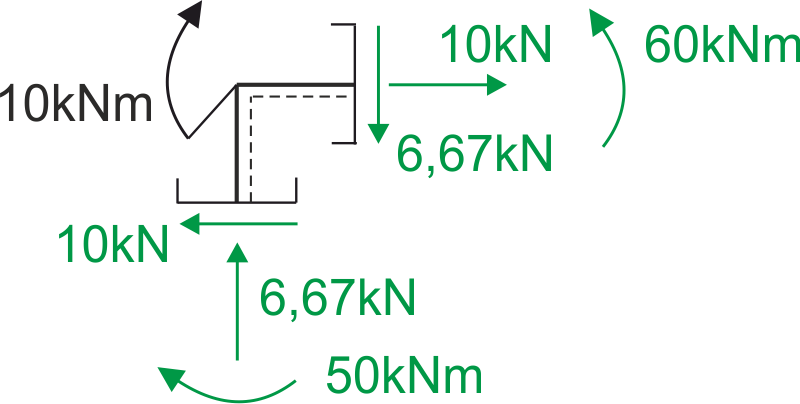
Rys7. Węzeł pierwszy - zaznaczone wszystkie siły przekrojowe
\begin{aligned} & \Sigma \mathrm{x}=0 \\ & -10+10=0 \\ & 0=0 \\ \\ & \Sigma \mathrm{y}=0 \\ & -6.67+6.67=0 \\ & 0=0 \\ \\ & \Sigma \mathrm{M}=0 \\ & 50-60+10=0 \\ & 0=0 \\ \end{aligned} Sprawdzenie daje pozytywny wynik.
Przykład 2
Równowaga węzła z prętem skośnym
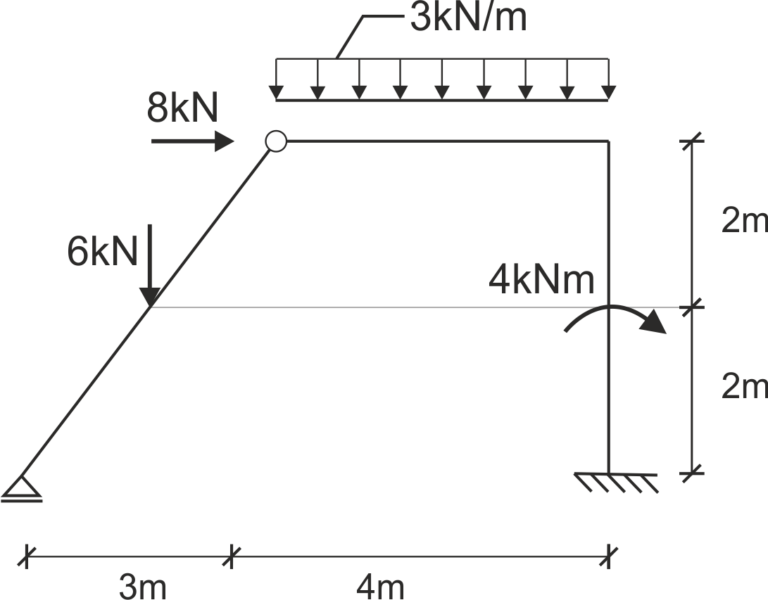
Rys8. Przykład 2 - temat
Wykresy sił wewnętrznych



Rys9. Wykresy sił wewnętrznych - przykład 2
Sprawdzenie równowagi węzła z prętem skośnym
Momenty w węźle się wyzerowały (przegub), więc nie mamy tutaj żadnych momentów, mamy siły tnące i normalne - odczytujemy je z narysowanych powyżej wykresów.Pamiętamy o konwencji znakowania, patrząc od prawej strony węzła C na wykresie sił normalnych mamy siłę -8kN, minus oznacza że jest to ściskanie, więc zaznaczamy siłę przy węźle od prawej strony z odpowiednim zwrotem.
Na wykresie sił tnących od prawej strony przy samym węźle mamy -3kN, patrząc od prawej strony dodatnie siły tnące mają zwrot w dół, więc ujemną siłę zaznaczamy ze zwrotem do góry.
W ten sam sposób odczytujemy zwroty i wartości sił z pręta skośnego. Jeśli przyjmiemy spody wewnątrz ramy, to musimy obrócić konwencję znakowania przeciwnie do ruchu wskazówek zegara o pewien kąt żeby dopasować ją do pręta skośnego, patrząc od lewej strony na konwencję znakowania widzimy jak zwrócone są dodatnie siły normalne i tnące od tej strony.
Na wykresie mamy siłę tnącą -3kN i siłę normalną +2,4kN. Tak wygląda wycięty węzeł z odczytanymi siłami przekrojowymi:

Rys10. Wycięty węzeł z prętem skośnym | \( \quad \quad \) | Równania równowagi statycznej \begin{aligned} &\Sigma X = 0\\ &8 - 8 - 2.4 \cdot \cos (\alpha) + 1.8 \cdot \sin (\alpha) = 0\\ &L = P\\ &\Sigma Y = 0\\ &3 - 2.4 \cdot \sin (\alpha) + 1.8 \cdot \cos (\alpha) = 0\\ &L = P \end{aligned} |
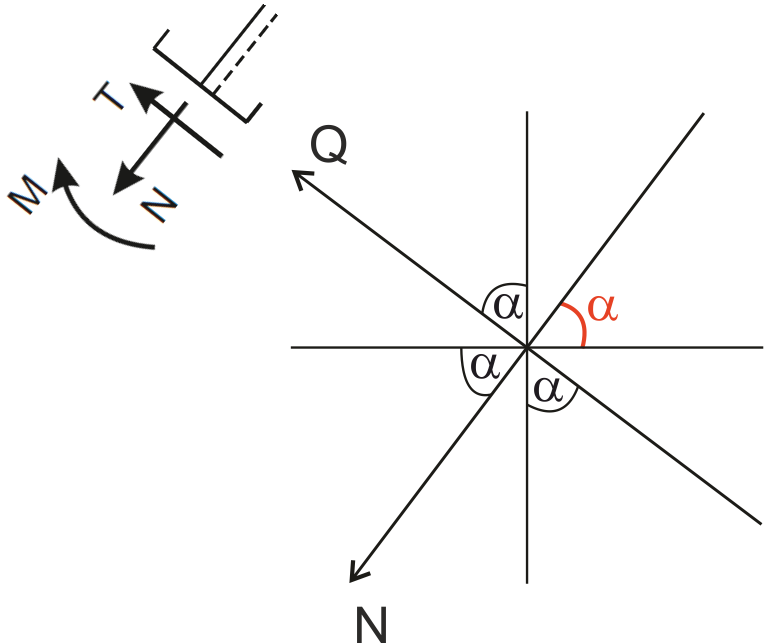
Rys11. Rysunek pomocniczy do rzutowania sił na składowe | \( \quad \quad \) | Jeśli chodzi o rzutowanie sił na składowe dobrym pomysłem jest narysować sobie taką "pajęczynę" - zrobić taki rysunek na którym zaznaczymy kierunek pionowy, poziomy, oś pręta (kierunek normalny) i prostopadłą do osi pręta (kierunek tnący). Kąt alfa przyjmuję patrząc na ramę między poziomem i osią pręta. Dodatkowo można sobie zaznaczyć zwrot dodatniej siły normalnej i dodatniej siły tnącej, który obowiązuje od tej strony od której patrzymy. |
Składowa przy której jest zaznaczony kąt alfa jest mnożona razy cosinus tego kąta, a ta druga razy sinus tego kąta.
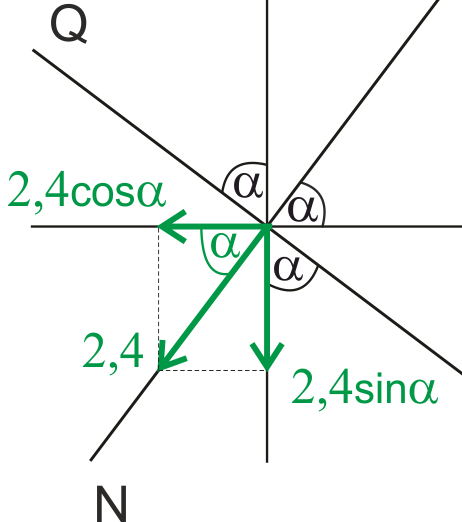
Rys12. Rzutowanie siły pod kątem na składowe x i y | \( \quad \quad \) |
Przykładowo do rzutowania siły normalnej na składowe moglibyśmy sobie to rozrysować tak jak na rysunku obok. |
Poniżej znajdziesz również odnośniki do licznych przykładów rozwiązania zarówno ram prostych jak i z prętem/prętami skośnymi, a także ramy w przegubami.
ZOBACZ TEŻ

