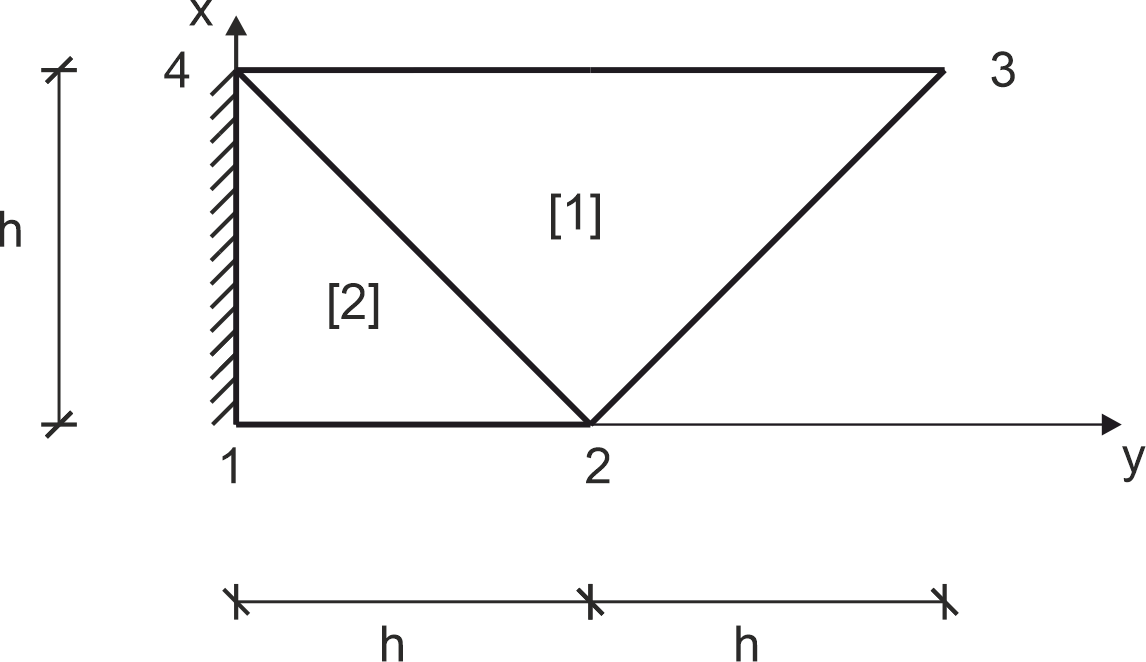
Obszar zdyskretyzowano 2 elementami skończonymi [1], [2] z węzłami ponumerowanymi jak na rysunku, \(\mathrm{h}=3.6\)
Dla zagadnienia Laplacea (stacjonarny przepływ ciepła) z wewnętrzenym źródłem ciepła w całym obszarze \(\mathrm{Q}=25\) [W/m^3] na cześci brzegu 1 - 4 przyjęto znanq temperaturę \(T=3.6 \cdot(x+y)\), na pozostałej części brzegu strumień ciepła \(\boldsymbol{q}=\mathbf{0}\).
Element [1] z węzłomi kolejno 2, 3, 4 ma macierz $$ \mathbf{K}^{e l 1}=27 \cdot\left[\begin{array}{rrr} 1 & -0.5 & -0.5 \\ -0.5 & 0.5 & 0 \\ -0.5 & 0 & 0.5 \end{array}\right] $$ Element [2] z węzłami kolejno 2, 4, 1 ma macierz $$ \mathbf{K}^{e / 2}=27 \cdot\left[\begin{array}{rrr} 0.5 & 0 & -0.5 \\ 0 & 0.5 & -0.5 \\ -0.5 & -0.5 & 1 \end{array}\right] $$
1. lle wynosi temperaturo w węźle 4?
2. lle wynosi drugi współczynnik wektora obciqżenia elementu [1]?
3. lle wynosi współczynnik \(\mathbf{K}_{22}\) globalnej macierzy sztywności?

Obszar w kształcie czworokąta zdyskretyzowono 2 elementami skończonymi ([1],[2]) z węzłami ponumerowanymi jak na rysunku. Niech \(\mathrm{h}=5\).
Dla zagadnienia Laplacea (stacjonarny przeptyw ciepła) obliczono stopnie swobody \(T_1=9, T_2=12, T_3=27, T_4=36\)
Jaka jest temperatura \(T_h\) w środku ciężkości elementu [1]?
Jaka jest pionowa składowa strumienia ciepła \(q_h\) w elemencie 2 |
Jaka byłaby składowa normalna strumienia ciepła na boku 2 - 3 gdyby strumień ciepła w elemencie [1] był równy [9 \sqrt{ } 2,27 \sqrt{2}] ? Przyjąć znak + jeżeli ciepło płynie do wnętrza obszaru.

Zastosować MES do rozwiązania (obliczenia stopni swobody) zagadnienia Laplace'a (\(f = 0\)) w obszarze zdyskretyzowanym dwoma jednakowymi elementami skończonymi \([1], [2]\) i węzłami ponumerowanymi jak na rysunku, \(h = 3\).

Przyjąć na części brzegu (1-2-3) warunki typu Dirichleta \( \hat{T} = 3y \) a na pozostałej części warunki typu Neumanna \( \hat{q} = 0 \).

Element \([1]\), z węzłami 1, 2, 4, ma macierz sztywności \( K^{el1} = \begin{pmatrix} -0.5 & -0.5 & 0 \\ -0.5 & 1 & -0.5 \\ 0 & -0.5 & 0.5 \end{pmatrix} \).

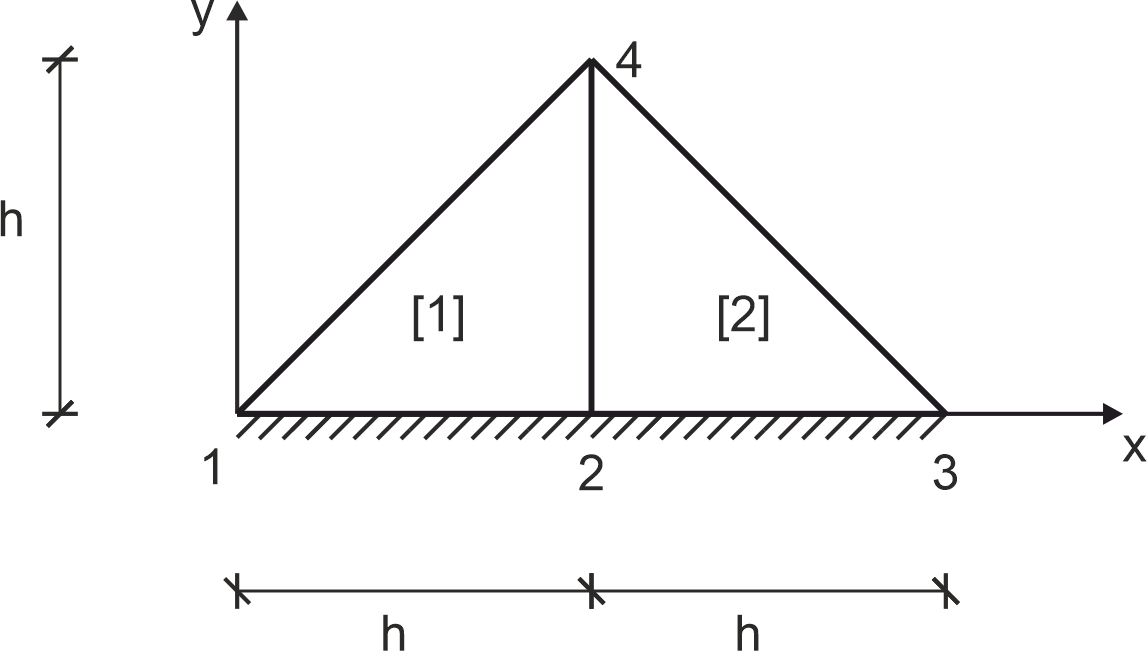
Zastosować MES do rozwiązania (obliczenia stopni swobody) zagadnienia Laplace'a (\(f = 0\)) w obszarze zdyskretyzowanym dwoma jednakowymi elementami skończonymi \([1], [2]\) i węzłami ponumerowanymi jak na rysunku, \(h = 2\).

Przyjąć na części brzegu (1-2-3) warunki typu Dirichleta \( \hat{T} = 2x \) a na pozostałej części warunki typu Neumanna \( \hat{q} = 0 \).

Element \([1]\), z węzłami 1, 2, 4, ma macierz sztywności \( K^{el1} = \begin{pmatrix} 0.5 & -0.5 & 0 \\ -0.5 & 1 & -0.5 \\ 0 & -0.5 & 0.5 \end{pmatrix} \).

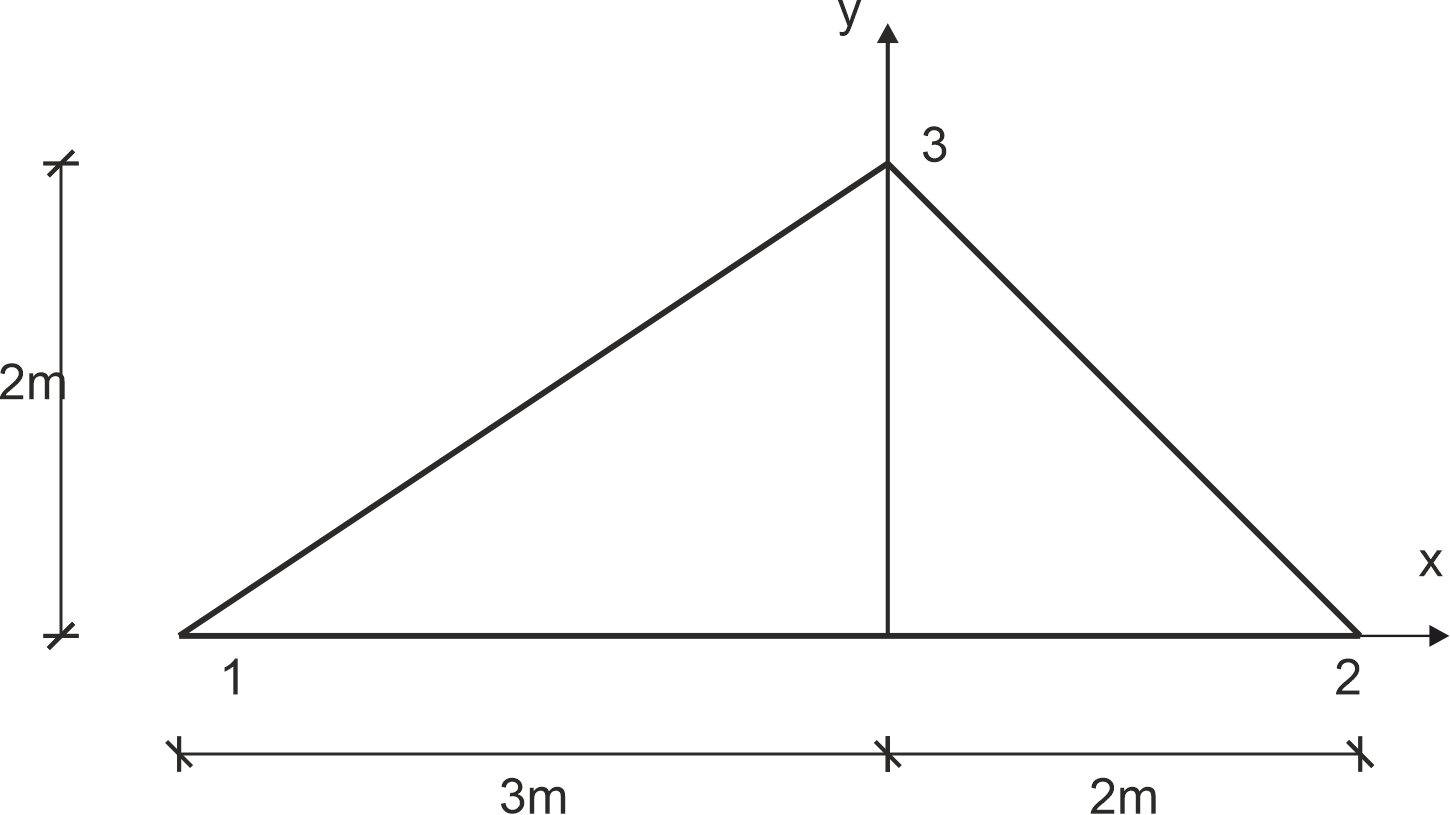
Dla elementu jak na rysunku znane są stopnie swobody: \( T_1 = -10 \), \( T_2 = -15 \), \( T_3 = 45 \). Napisać wzór na temperaturę wzdłuż wysokości poprowadzonej z wierzchołka 3. Jaka jest temperatura w środku ciężkości tego elementu?