Lista zadań
Przykład 1
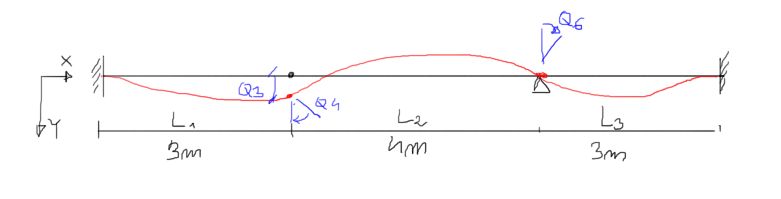
Dony jest wektor rozwiqzanio $\mathbf{Q}$ dla belki podzielonej no 3 elementy skoríczone jok no schemocie ponizei. Stosujqc MES oblicz wortośc ugięcia dlo $X-9 \mathrm{~m}$. $\mathbf{Q}=\left\{\begin{array}{llllllll}0 & 0 & 2,5 & 2 & 0 & 6 & 0 & 0\end{array}\right\} \cdot 10^{2}$
Przykład 2

Dla belki o schemacie jak na rysunku, sztywności giętnej \(E I=3600 \mathrm{kNm}^2\) oraz równych przęsłach długości 6 m , przy obciążeniu rozlożonym \(p=10 \mathrm{kN} / \mathrm{m}\) i osiadaniu skrajnej podpory o \(\Delta=0.02 \mathrm{~m}\), obliczyć niezerowe przemieszczenie węzłowe. Naszkicować ugięcia belki.
Przykład 3

Dla belki o schemacie jak na rysunku, sztywności giętnej \(E J=1125 \mathrm{kNm}^2\) oraz równych przęsłach długości 3 m , przy obciążeniu rozłożonym \(p=4 \mathrm{kN} / \mathrm{m}\) i sile skupionej \(P_5=9 \mathrm{kN}\) po prawej stronie, oblicz przemieszczenia węzłowe i naszkicuj deformację belki.
Przykład 4
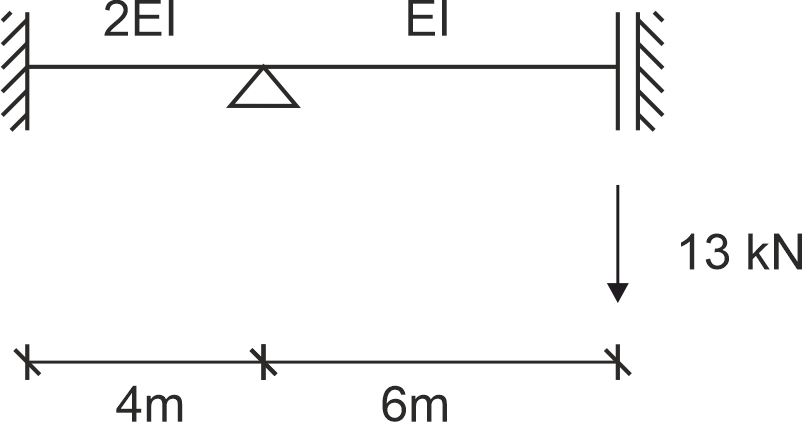
Rozwiązać belkę jak na rysunku metodą elementów skończonych (obliczyć wektory przemieszczeń i reakcji oraz wykonać wykresy sił przekrojowych). \(EI=18000 kNm^2\)
Przykład 5
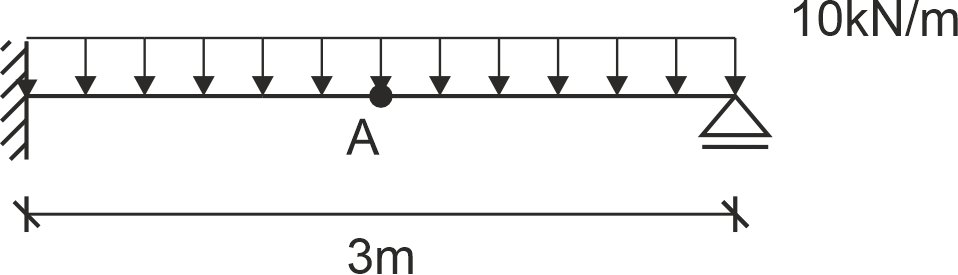
Rozwiązać poniższą konstrukcję metodą elementów skończonych
\[ EA = 3 \cdot 10^5 \, \text{kN} \quad EI = 250 \, \text{kNm}^2 \]
1. Obliczyć wektor przemieszczeń
2. Obliczyć wektor reakcji
3. Wykonać wykresy
4. Obliczyć ugięcie w punkcie A (w połowie elementu)