Lista zadań
Przykład 2
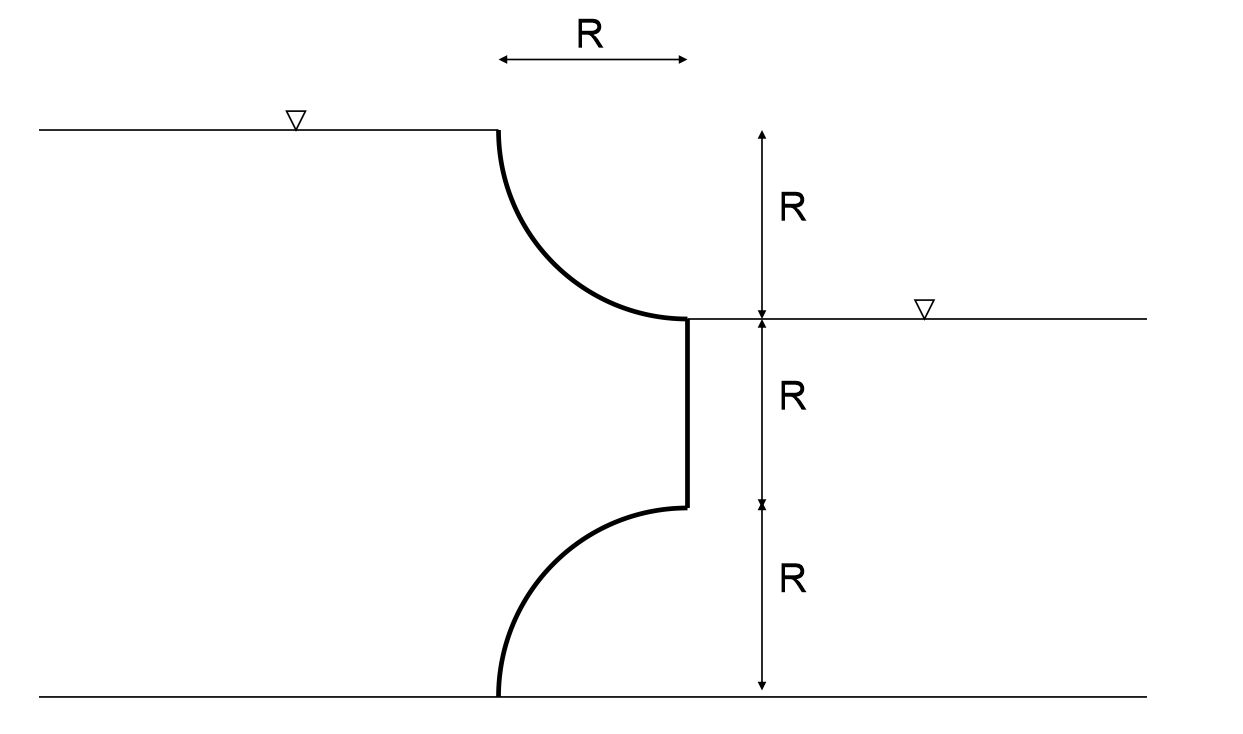
Narysuj wykresy parcia i oblicz wartość parcia. Szerokość zbiornika b=2m.
Przykład 3
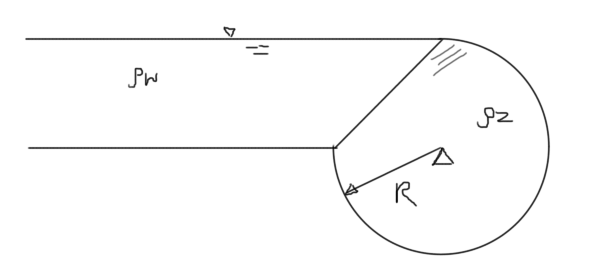
Zawór o promieniu R=1 m i długości L=10 m zamyka naroże prostopadłościennego zbiorniku jak na rysunku. Wyznaczyć moment jakim należy utrzymywać zawór w pozycji zamkniętej, jeżeli zbiornik napełniono wodą o gęstości \(\rho_w=1 g/cm^3\), natomiast gęstość materiału z którego wykonano zawór wynosi \(\rho_z=5 g/cm^3.\)
Przykład 4
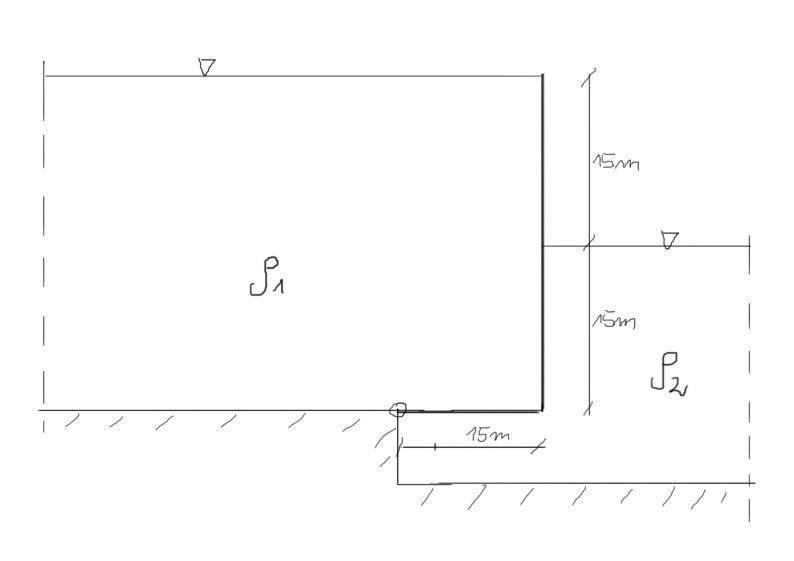
Ile razy musi być większa gęstość cieczy nr 2 w stosunku do gęstości cieczy nr 1, aby nastąpiła równowaga? Szerokość zbiornika \( b=1m \)
Przykład 5
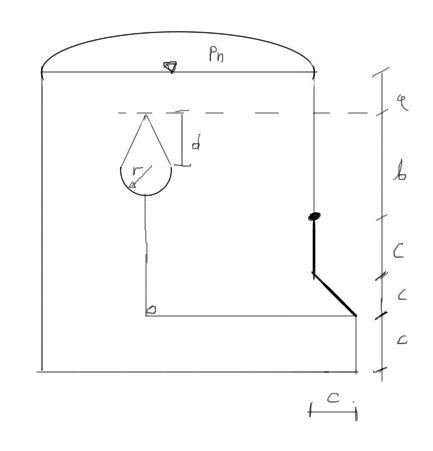
W bocznej ścianie zbiornika, w którym panuje nadciśnienie \( p_n=4905 Pa \) znajduje się otwór. Otwór jest zamykany płaską klapą o szerokości L za pomocą pływaka w kształcie stożka o wysokości d połączonego z połówką kuli o promieniu r. Klapa może obracać się względem punktu O. Pływak ma masę m. Wzniesienie wierzchołka pływaka nad oś obrotu klapy wynosi b. Wierzchołek pływaka zanurzony jest na głębokości a. Jaką objętość V musi mieć pływak, aby zapewnić zamknięcie otworu jak na rysunku?
Dane: \(
a=0,25m,
b=0,75m,
c=0,5m,
m=10kg,
\rho_{H_2O} = 1000 kg/m^3,
L=0,5m,
p_n=4905Pa
\)
Przykład 6
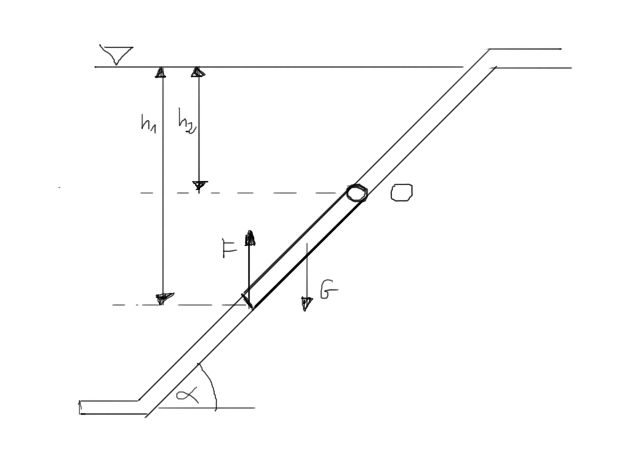
Kwadratowa klapa o ciężarze G przykrywa otwór spustowy zbiornika wodnego. Klapa posiada oś obrotu O. Określić pionową siłę F potrzebną do podniesienia klapy.
Dane:
\begin{aligned}
&h_1 = 3.5 m\\
&h_2 = 2.5 m\\
&G = 200 N\\
&\alpha = 30^{\circ}\\
\end{aligned}
Przykład 7
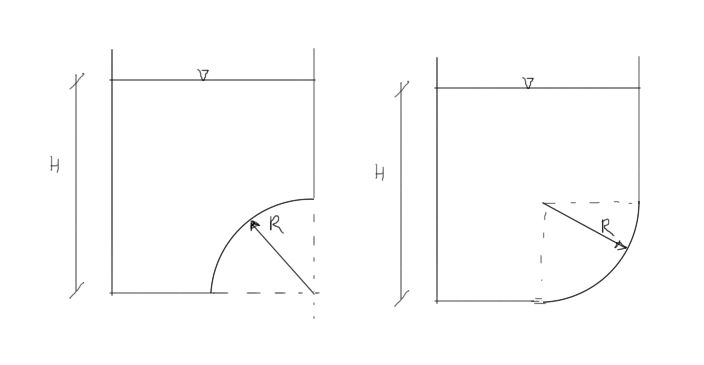
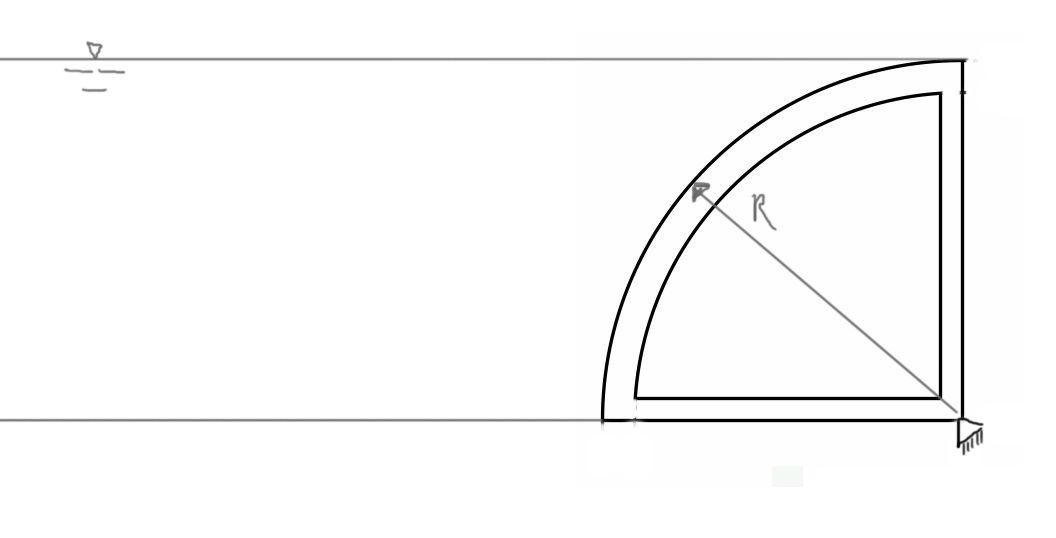
Zbiornik zamknięto klapą obrotową w kształcie ćwiartki walca o promienu R=1m i długości L=1m. Wyznaczyć wielkość naporu hydrostatycznego wywieranego na klapę dla dwóch wariantów pokazanych na rysunku. Gęstość wody \(\rho = 1000 kg/m^3 \), wysokość wody w zbiorniku H=2m.
Przykład 8
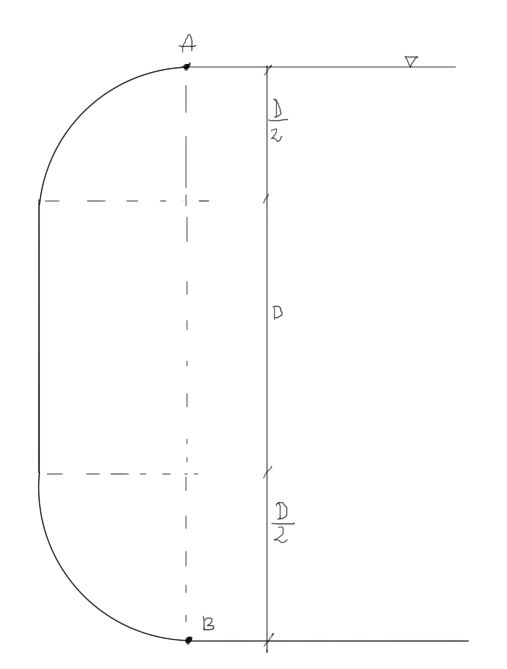
Oblicz parcie wody na powierzchnię AB zamknięcia o kształcie pokazanym na rysunku. Dane: \begin{aligned} &D = 2m\\ &B = 5m\\ \end{aligned}
Przykład 9
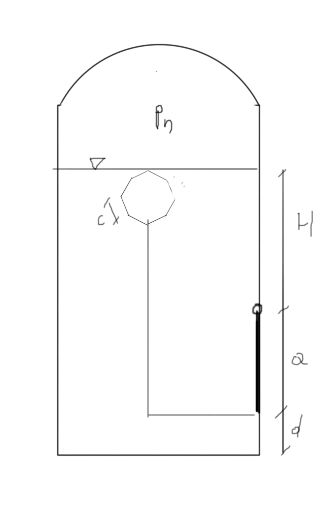
W bocznej ścianie zbiornika, w którym panuje nadciśnienie \( p_n = 200 hPa \) znajduje się prostokątny otwór o wymiarach \( a \times a/2 \). Otwór zamykany jest płaską klapą za pomocą pływaka o kształcie graniastosłupa o podstawie sześciokąta foremnego o boku c i wysokości f. Pływak ma masę \( m_p = 10 kg \). Wzniesienie wody nad osią obrotu klapy wynosi \( H \). Jaką objętość \( V \) musi mieć pływak, aby zapewnić zamknięcie otworu przy całkowitym zanurzeniu pływaka?
Dane:
\begin{aligned}
&a=0,8 m\\
&b=1 m \\
&c=0,7 m\\
&H =2 m\\
\end{aligned}
Przykład 10
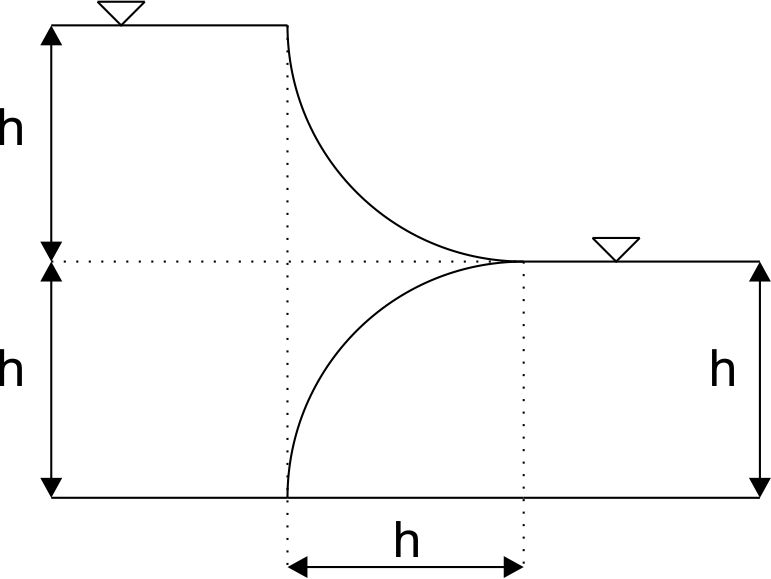
Dla układu jak na rysunku oblicz wartość parcia, położenia punktu parcia oraz kąt pod jakim działa siła parcia. \begin{aligned} & \rho=1000 \frac{\mathrm{kg}}{\mathrm{m}^3} \\ & g=9.81 \frac{m}{s^2} \\ & \gamma=\rho \cdot g=9810 \frac{N}{m^3} \\ & h=1 m \\ & b=1 m \end{aligned}
Przykład 11
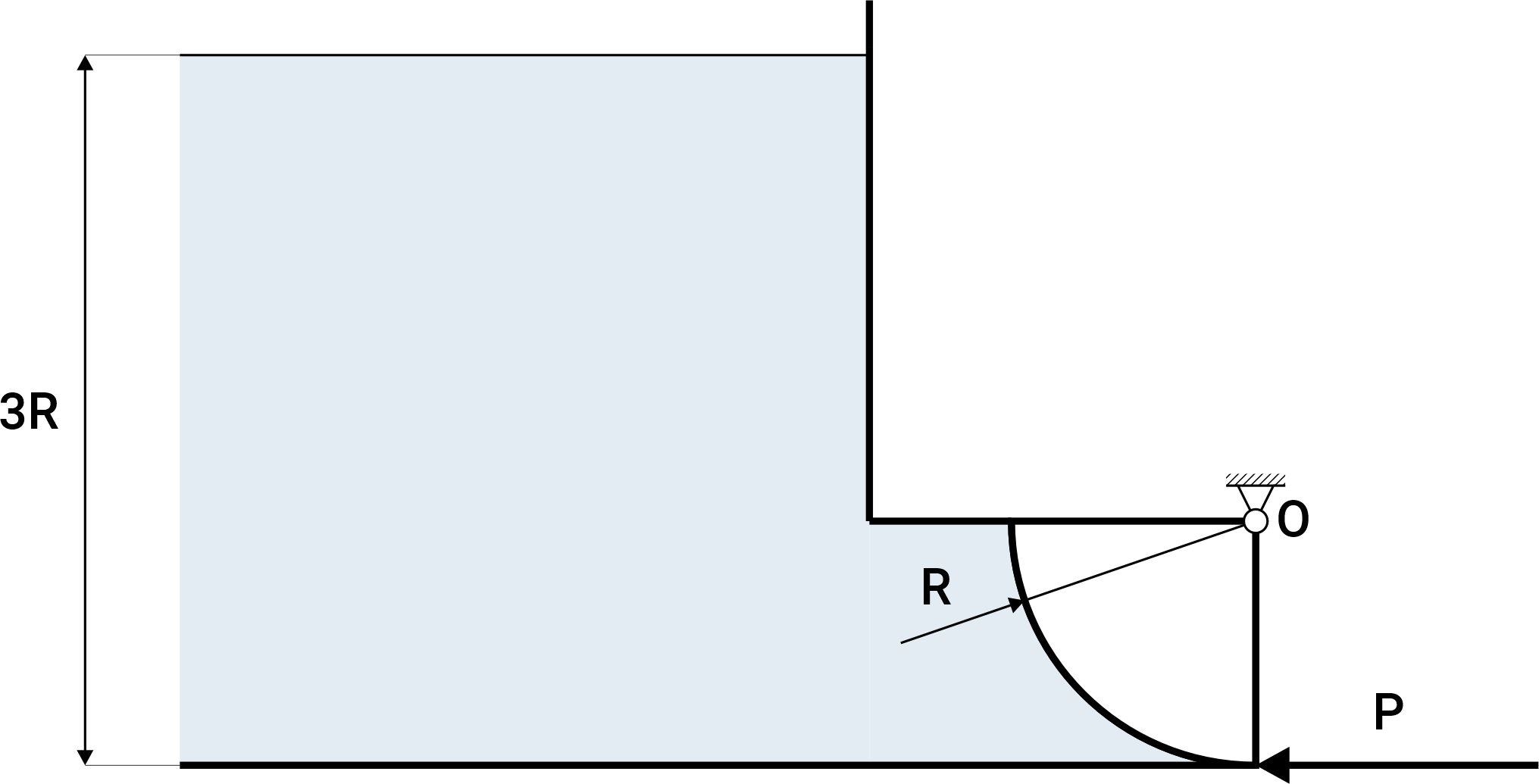
Zawór w kształcie \(1 / 4\) walca, wykonany z materiału o gęstości \(\rho_{\mathrm{z}}=7 \mathrm{~g} / \mathrm{cm}^3\), który może się obracać wokół osi „O” zamyka prostokątną rurę o szerokości \(\mathbf{B}=\mathbf{2} \mathbf{R}\) i wysokości \(\mathbf{R}=\mathbf{1 m}\), którą woda może wypływać z basenu. Wyznaczyć wartość siły \(\boldsymbol{P}\) niezbędnej do utrzymania zaworu w pozycji zamkniętej, jeżeli basen wypełniono wodą do wysokości \(3 R\). Przyjąć gęstość wody \(\rho=1 \mathrm{~g} / \mathrm{cm}^3\).