Diagrammes dans les Poutres
Dans ce texte, vous apprendrez ce qu’est une force axiale (normale), une force tranchante et un moment fléchissant, ainsi que la convention de signe de ces efforts internes.
Nous décrirons quelles sont les relations entre la charge distribuée, la force tranchante et le moment fléchissant, et quels changements on doit s’attendre à voir dans les diagrammes d’efforts internes pour une charge donnée sur la poutre.
Voici la convention de signe généralement utilisée pour chacun des efforts internes :

1. Effort normal (N)
2. Effort tranchant (Q)
3. Moment fléchissant (M)
Lien entre :
Elle peut être constante ou variable selon la position x sur la poutre.
\( \frac{dQ(x)}{dx} = -q(x) \)
En d’autres termes, la variation de l’effort tranchant le long de la poutre est causée par la charge distribuée.
\( \frac{dM(x)}{dx} = Q(x) \)
Ainsi, la variation du moment fléchissant le long de la poutre est due à l’effort tranchant.
1) La méthode de base pour tracer les diagrammes d’efforts internes consiste à d’abord écrire les fonctions d’efforts internes. Dans nos cours, y compris nos ressources gratuites, vous trouverez des exemples montrant la résolution complète d’une poutre par cette méthode.
2) Une méthode plus avancée consiste à tracer les diagrammes sans écrire les fonctions d’efforts internes, et pour cette méthode il est utile de connaître certaines règles pour tracer les diagrammes d’efforts internes :
3) Un lien intéressant entre Q(x) et M(x) — à savoir que la variation du diagramme de moment fléchissant correspond à l’aire sous le diagramme de l’effort tranchant — peut également être exploité pour tracer les diagrammes. Des calculs qui utilisent cette méthode se trouvent dans nos documents sur YouTube, bien qu’elle soit rarement présentée par les enseignants.
La théorie, c’est bien, mais la meilleure compréhension vient souvent de la résolution d’exemples :
Un cours vidéo montrant comment déterminer les sauts sur les diagrammes
Nous décrirons quelles sont les relations entre la charge distribuée, la force tranchante et le moment fléchissant, et quels changements on doit s’attendre à voir dans les diagrammes d’efforts internes pour une charge donnée sur la poutre.
Calcul des poutres
Types d’efforts internes
Nous avons trois types fondamentaux d’efforts internes qui peuvent apparaître dans les poutres :
1. Efforts normaux (axiaux) – résultent de l’action de forces le long de l’axe de la poutre. Si la force est dirigée le long de l’axe de la poutre, provoquant traction ou compression, il s’agit d’un effort normal. Symboliquement noté N.
2. Efforts tranchants – agissent perpendiculairement à l’axe de la poutre et génèrent des contraintes de cisaillement internes. Notés Q, ils sont responsables du déplacement vertical entre différentes sections de la poutre.
3. Moment fléchissant – c’est le moment d’une force qui provoque la flexion de la poutre. Il influe sur la courbure de la poutre et varie le long de sa longueur. Le moment fléchissant est noté M.
2. Efforts tranchants – agissent perpendiculairement à l’axe de la poutre et génèrent des contraintes de cisaillement internes. Notés Q, ils sont responsables du déplacement vertical entre différentes sections de la poutre.
3. Moment fléchissant – c’est le moment d’une force qui provoque la flexion de la poutre. Il influe sur la courbure de la poutre et varie le long de sa longueur. Le moment fléchissant est noté M.
Convention de signe pour les efforts internes
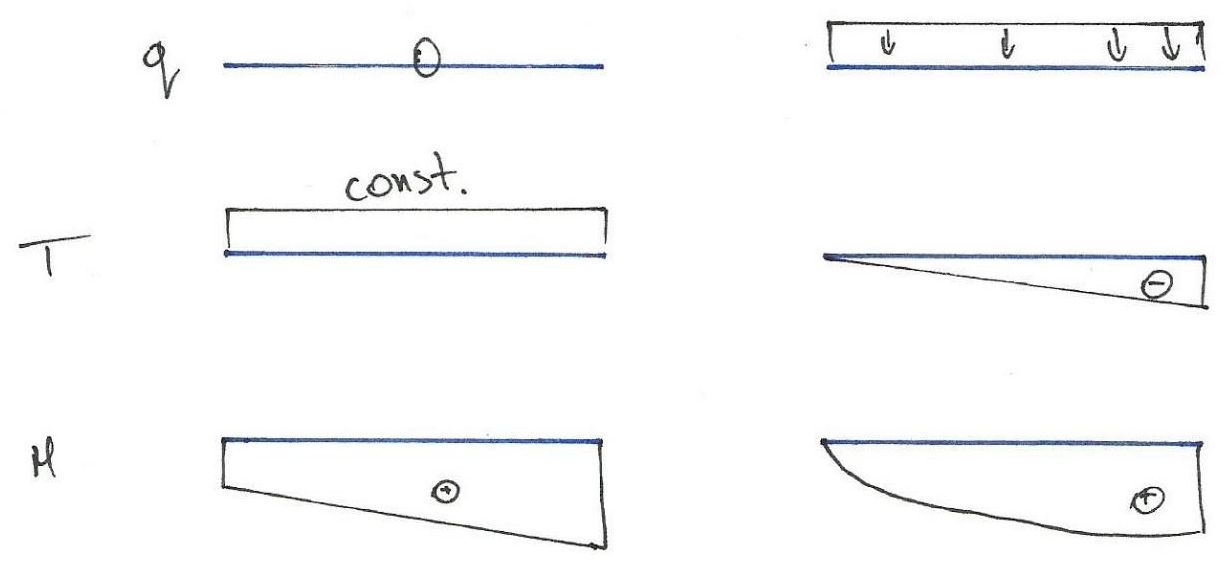
La convention de signe pour les efforts internes dans la mécanique des poutres est essentielle pour interpréter correctement leurs directions et leurs valeurs, ainsi que pour consigner les résultats de manière cohérente dans l’analyse des structures.Voici la convention de signe généralement utilisée pour chacun des efforts internes :

Fig. 1. Convention de signe pour les efforts internes
1. Effort normal (N)
- Traction : Une force qui étire la poutre (agissant vers l’extérieur de la section, “s’éloignant” du centre de la poutre) est généralement considérée comme positive. En bref : si la poutre est en traction, l’effort normal N est positif.
- Compression : Une force qui comprime la poutre (agissant axialement vers l’intérieur de la section, provoquant une compression) est considérée comme négative.
- Compression : Une force qui comprime la poutre (agissant axialement vers l’intérieur de la section, provoquant une compression) est considérée comme négative.
2. Effort tranchant (Q)
- Effort tranchant positif : Lorsque l’effort agit vers le haut sur le côté gauche de la section ou vers le bas sur le côté droit de la section, l’effort tranchant est considéré comme positif.
- Effort tranchant négatif : L’effort agissant vers le bas sur le côté gauche de la section ou vers le haut sur le côté droit de la section est considéré comme négatif.
- Effort tranchant négatif : L’effort agissant vers le bas sur le côté gauche de la section ou vers le haut sur le côté droit de la section est considéré comme négatif.
3. Moment fléchissant (M)
- Moment fléchissant positif (moments qui provoquent un “sourire”) : Si le moment fléchissant fait que la poutre se déforme en forme de “sourire” (c.-à-d. les fibres supérieures de la poutre sont comprimées et les fibres inférieures sont en traction), le moment est positif.
- Moment fléchissant négatif (moments qui provoquent une “mine triste”) : Lorsque la poutre se déforme dans l’autre sens (les fibres supérieures en traction et les fibres inférieures en compression — une “mine triste”), le moment fléchissant est négatif.
- Moment fléchissant négatif (moments qui provoquent une “mine triste”) : Lorsque la poutre se déforme dans l’autre sens (les fibres supérieures en traction et les fibres inférieures en compression — une “mine triste”), le moment fléchissant est négatif.
Lien entre :
charge distribuée <-> effort tranchant <-> moment fléchissant
1. Charge distribuée q(x)
La charge distribuée q(x) est une force répartie le long de la poutre, agissant par unité de longueur.Elle peut être constante ou variable selon la position x sur la poutre.
2. Effort tranchant Q(x)
Le lien entre la charge distribuée et l’effort tranchant est :\( \frac{dQ(x)}{dx} = -q(x) \)
En d’autres termes, la variation de l’effort tranchant le long de la poutre est causée par la charge distribuée.
- Lorsque la charge distribuée q(x) est positive (p. ex. dirigée vers le bas), l’effort tranchant Q(x) diminue le long de la poutre.
- Lorsque q(x) = 0 (absence de charge), l’effort tranchant est constant.
- Si l’effort tranchant est nul, alors le moment fléchissant est constant.
- Lorsque q(x) = 0 (absence de charge), l’effort tranchant est constant.
- Si l’effort tranchant est nul, alors le moment fléchissant est constant.
3. Moment fléchissant M(x)
Le lien entre l’effort tranchant et le moment fléchissant est :\( \frac{dM(x)}{dx} = Q(x) \)
Ainsi, la variation du moment fléchissant le long de la poutre est due à l’effort tranchant.
- Lorsque l’effort tranchant Q(x) est positif, le moment fléchissant M(x) augmente.
- Lorsque sur le diagramme d’effort tranchant Q(x) = 0, le moment fléchissant atteint un extremum.
- Lorsque sur le diagramme d’effort tranchant Q(x) = 0, le moment fléchissant atteint un extremum.

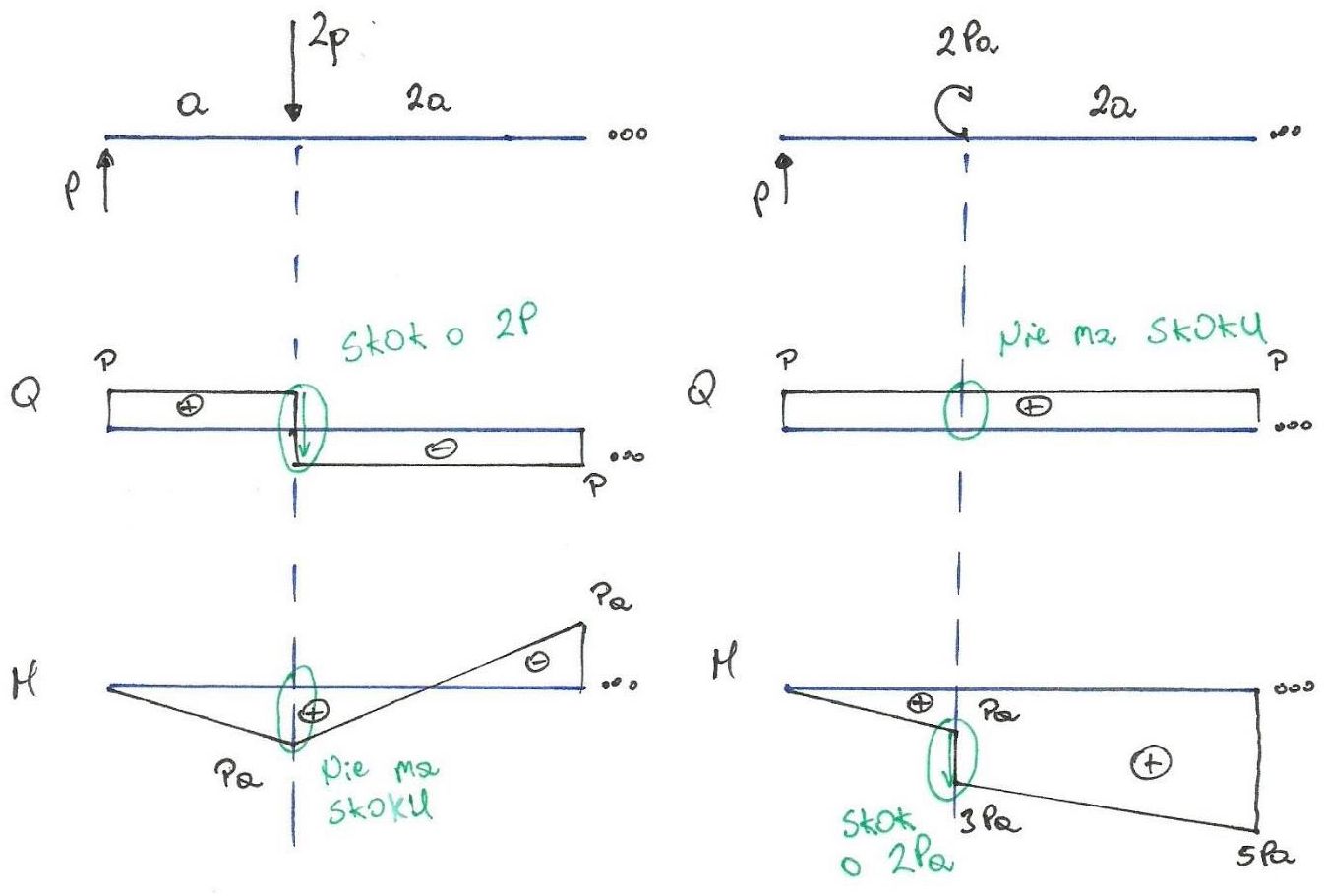
Fig. 2. Lien : charge distribuée – effort tranchant – moment fléchissant
Règles pour tracer les diagrammes d’efforts internes
Disons qu’il existe trois méthodes pour tracer les diagrammes d’efforts internes :1) La méthode de base pour tracer les diagrammes d’efforts internes consiste à d’abord écrire les fonctions d’efforts internes. Dans nos cours, y compris nos ressources gratuites, vous trouverez des exemples montrant la résolution complète d’une poutre par cette méthode.
2) Une méthode plus avancée consiste à tracer les diagrammes sans écrire les fonctions d’efforts internes, et pour cette méthode il est utile de connaître certaines règles pour tracer les diagrammes d’efforts internes :
- Si en un point quelconque de la poutre une force transversale est appliquée, il se produit un saut sur le diagramme d’effort tranchant Q égal à la valeur de cette force,
le saut va dans le sens de la force quand on lit le diagramme de gauche à droite,
- Si un tronçon de la poutre subit une charge distribuée, alors sur le diagramme d’effort tranchant Q de ce tronçon se produit une variation égale à la résultante de la charge distribuée,
avec un sens conforme à cette résultante (en lisant de gauche à droite),
- Si en un point quelconque de la poutre un moment ponctuel est appliqué, il se produit un saut sur le diagramme du moment M égal à la valeur de ce moment,
ce saut est positif ou négatif selon qu’il soit horaire ou antihoraire — voir la convention de signe.
le saut va dans le sens de la force quand on lit le diagramme de gauche à droite,
- Si un tronçon de la poutre subit une charge distribuée, alors sur le diagramme d’effort tranchant Q de ce tronçon se produit une variation égale à la résultante de la charge distribuée,
avec un sens conforme à cette résultante (en lisant de gauche à droite),
- Si en un point quelconque de la poutre un moment ponctuel est appliqué, il se produit un saut sur le diagramme du moment M égal à la valeur de ce moment,
ce saut est positif ou négatif selon qu’il soit horaire ou antihoraire — voir la convention de signe.

Fig. 3. Chargement sur la poutre et sauts sur les diagrammes Q et M
3) Un lien intéressant entre Q(x) et M(x) — à savoir que la variation du diagramme de moment fléchissant correspond à l’aire sous le diagramme de l’effort tranchant — peut également être exploité pour tracer les diagrammes. Des calculs qui utilisent cette méthode se trouvent dans nos documents sur YouTube, bien qu’elle soit rarement présentée par les enseignants.
La théorie, c’est bien, mais la meilleure compréhension vient souvent de la résolution d’exemples :
Un cours vidéo montrant comment déterminer les sauts sur les diagrammes
et décrivant les méthodes 2) et 3) de tracé de diagrammes au moyen de 4 exemples.
Ensemble de 19 poutres avec solutions succinctes
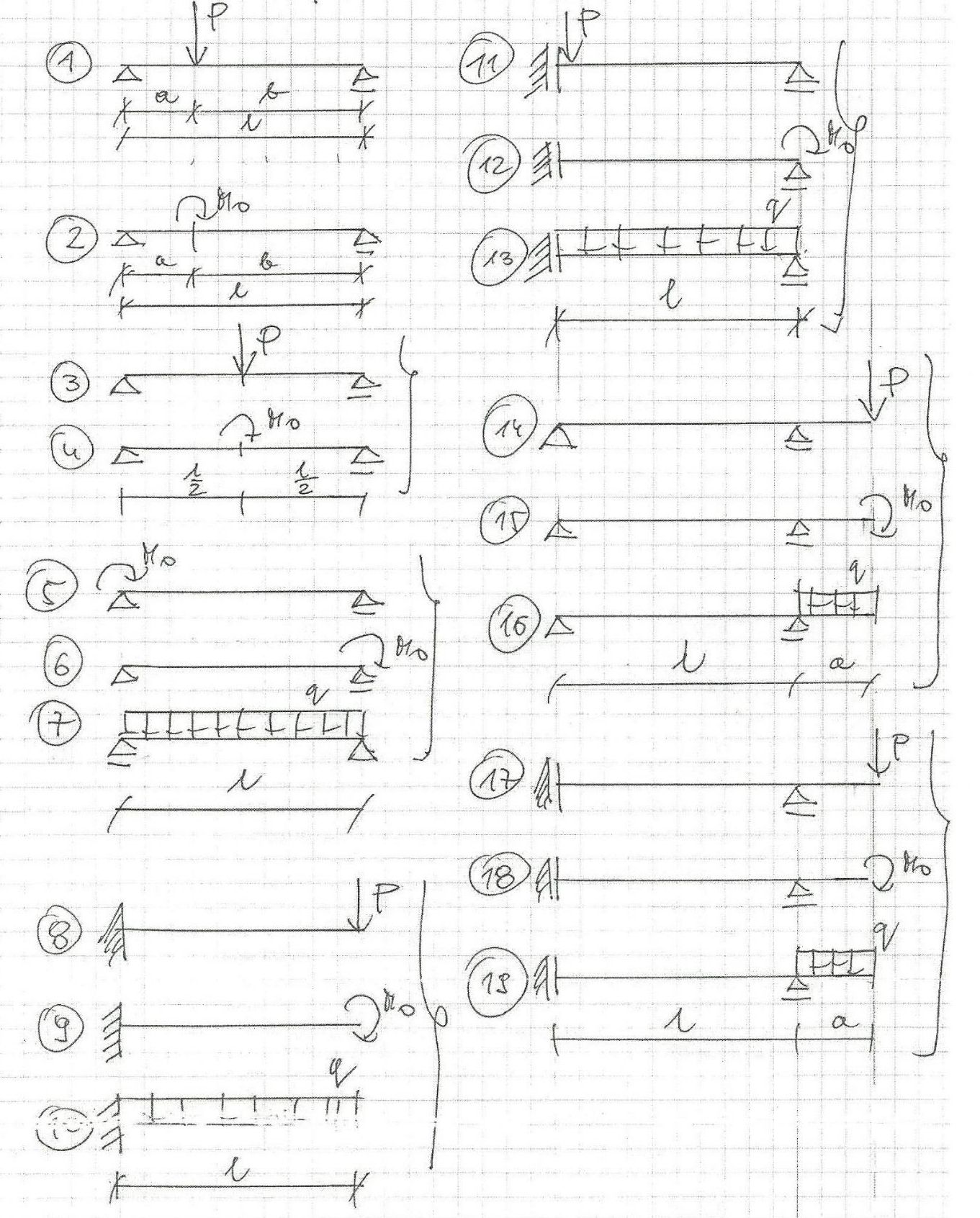
Voici les solutions brèves + diagrammes pour chaque poutre
Solutions












Ci-dessous, vous trouverez également des liens vers de nombreux exemples de solution pour des poutres droites, inclinées et articulées.