Résistance des matériaux - Méthode de Clebsch
- E - module de Young,
- J - moment d'inertie de la section de la poutre par rapport à l'axe horizontal.
Le signe « - » à droite de l'équation résulte du système de coordonnées adopté
et de la convention définissant le signe du moment fléchissant.
Concrètement - l'hypothèse des flèches positives vers le bas, donc d'une direction positive de l'axe de déformation vers le bas.
Pour déterminer les flèches de la poutre, nous intégrons deux fois l'équation ci-dessus
et obtenons la première dérivée - la fonction de l'angle de rotation de la poutre
et la deuxième dérivée - la fonction de déformation
C et D désignent les constantes d'intégration.
Les constantes d'intégration sont déterminées par les conditions aux limites cinématiques, c'est-à-dire les conditions sur les flèches nulles et les angles de déformation dans un type de support donné. Voir quels sont les types de supports pour une poutre dans le plan
Comme nous l'avons remarqué, la méthode de Clebsch, en respectant certaines conditions de notation, permet pour une poutre simple d'obtenir l'équation de la ligne de déformation contenant seulement deux inconnues (constantes d'intégration) indépendamment du nombre de segments.
Les principes régissant l'application de la méthode de Clebsch peuvent être résumés en 4 points :
- les sections dans tous les segments doivent être mesurées à partir du même point
nous adoptons pour la poutre simple un seul système de coordonnées, nous ne pouvons pas écrire par exemple une partie de la fonction d'un côté et une partie de l'autre côté de la poutre
- en cas d'application d'une charge continue, celle-ci ne peut pas être interrompue
si un tel cas se présente, la charge continue doit être prolongée jusqu'à l'extrémité de la poutre, en ajoutant en même temps une charge identique, avec un signe opposé (contre-charge)
- tous les nouveaux termes entrant dans l'expression du moment fléchissant doivent contenir le facteur \( (x- l_{i-1}) \),
où :
\(l_{i-1}\) désigne la coordonnée du début du i-ème segment de la poutre
- en cas d'apparition d'un moment concentré M – nous multiplions le moment par le bras d'action à la puissance 0
- l'intégration doit être effectuée sans développer les expressions dans les parenthèses
les constantes d'intégration s'appliquent à l'ensemble de la poutre (pour tous les segments)
Si les coordonnées \(l_{\mathrm{i}}\) déterminent la position des forces concentrées \(P_{\mathrm{i}}\)
ou des débuts de charge continue \(q_{\mathrm{i}}\),
alors des expressions du type \(P_i\left(x-l_i\right)\) ou \(q_i \frac{\left(x-l_i\right)^2}{2}\) sont intégrées selon le schéma
Dans ce cours, vous apprendrez
Méthode de Clebsch (analytique) :- comment déterminer la fonction de moment pour la poutre selon la méthode de Clebsch,
- comment écrire l'équation différentielle de l'axe déformé et comment l'intégrer,
- comment calculer les constantes d'intégration de l'équation à partir des conditions aux limites pour différents types de poutres,
- comment calculer la flèche et l'angle de rotation à un point donné de la poutre.
Systèmes statiquement indéterminés :
- comment déterminer les réactions dans une poutre statiquement indéterminée par la méthode de Clebsch.
Et maintenant, regardons l'exemple ci-dessous et voyons la solution en pratique.
Voir l'exemple
Poutre à trois segments avec différents types de charges.
Calculer la flèche et l'angle de rotation à un point donné de la poutre.
Solution de l'exemple du cours vidéo
Énoncé
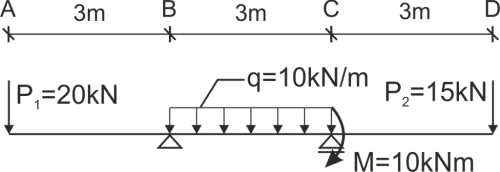
Solution
Nous calculons les réactions d'appui
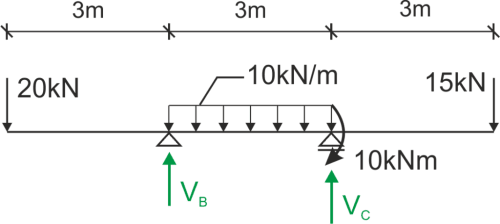 \begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
\begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
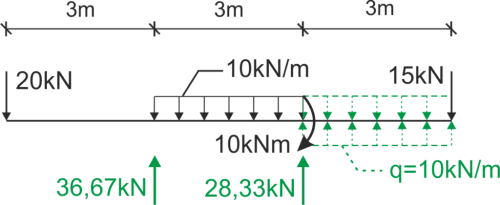
Nous écrivons la fonction de moment du côté gauche.
La fonction peut également être écrite du côté droit. Nous vous encourageons à vérifier cette variante, à calculer le déplacement recherché et à comparer les résultats.
 \begin{aligned}
&M_g(x)=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\
&EJ\cdot w"=-M_g(x)=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\
&EJ\cdot w'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\
&EJ\cdot w=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\
\end{aligned}
\begin{aligned}
&M_g(x)=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\
&EJ\cdot w"=-M_g(x)=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\
&EJ\cdot w'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\
&EJ\cdot w=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\
\end{aligned}
Conditions aux limites
\begin{aligned} &w(x=3)=0 \Rightarrow 90+3C+D=0\\ &w(x=6)=0 \Rightarrow 588.735+6C+D=0\\ &C=-166,245\\ &D=408.735\\ \end{aligned}Nous calculons la flèche au point A.
Si nous avons adopté le système de coordonnées à l'extrémité gauche de la poutre, alors le point A a la coordonnée x=0.
Par conséquent \begin{aligned} &w_A(x=0)=\frac{1}{EI}\cdot (D)\\ \end{aligned} \begin{aligned} &w_A=\frac{1}{EI}\cdot (408.735)\\ \end{aligned}