Lista zadań
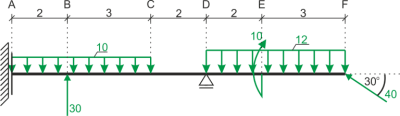
Exemple 1
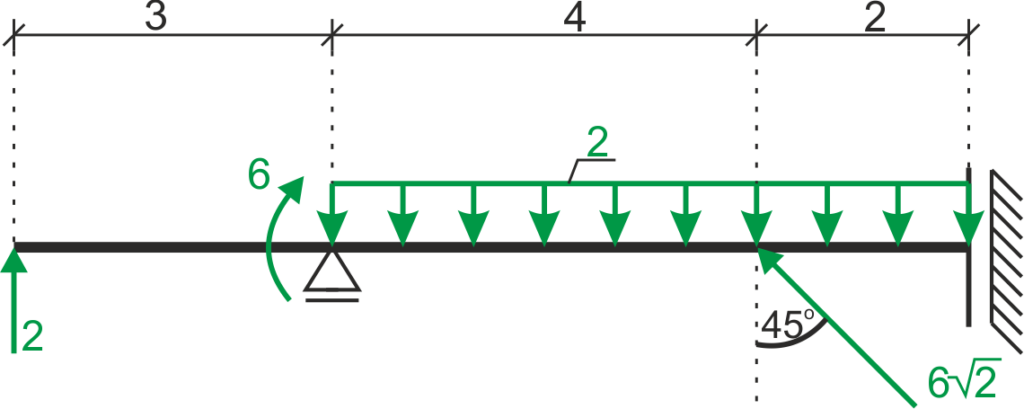
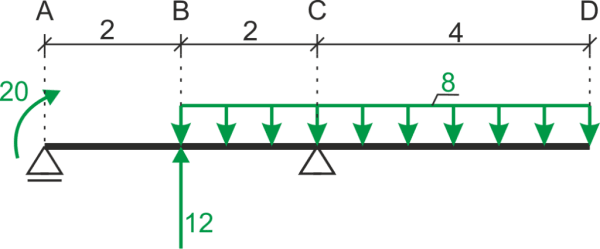
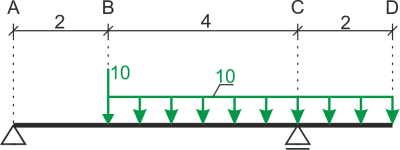
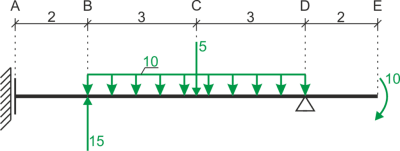
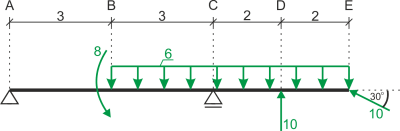
Déterminer et dessiner les diagrammes de forces internes.
Exemple 14

Dans la poutre présentée dans l'image, on enregistre le moment de flexion M₉₉₉subscript{g}(x) sur le segment BA(L ≤ x ≤ 3L) comme une fonction polynomiale du troisième degré de la variable indépendante x. On suppose M = 4500 [kNm], R = 450 [kN]. De plus, déterminez le point et la valeur extrême du moment de flexion dans l'intervalle AB. On suppose les valeurs suivantes : charge répartie q = 10 [kN/m] et longueur L = 10 [m].