Une poutre librement supportée d'une section représentée dans le dessin ci-dessous est chargée d'une force P = 100 kN. Vérifiez les valeurs des contraintes au niveau des points critiques de la section dangereuse. Utilisez l'hypothèse HMH dans les calculs. Tracez les diagrammes des moments de flexion et des efforts tranchants ainsi que la répartition des contraintes le long de la hauteur de la section. Les contraintes admissibles sont respectivement \(k_r=120\ MPa, k_c=80\ MPa\).

Une poutre librement supportée, dont la section est représentée sur le schéma ci-dessous, est soumise à une force de 30 kN. Réaliser les graphiques des moments de flexion et des forces transverses, ainsi que la répartition des contraintes le long de la hauteur de la section.

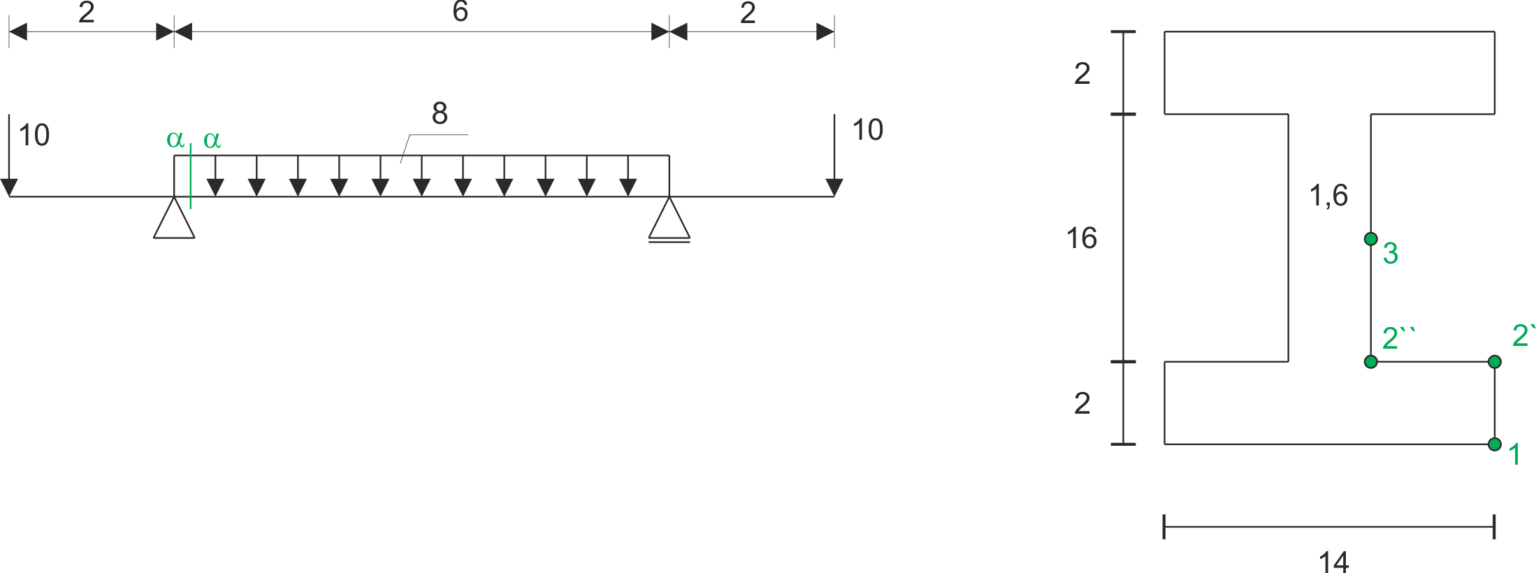
Une poutre librement fixée, dont la section est représentée dans le schéma ci-dessous, est chargée symétriquement par des forces concentrées et une charge continue. Tracer les diagrammes des moments fléchissants et des forces transversales, ainsi que la répartition des contraintes le long de la hauteur de la section.

Une poutre librement soutenue avec une section représentée dans le schéma ci-dessous est soumise à une charge continue. Dessinez des graphiques des moments de flexion et des forces transversales ainsi que la répartition des contraintes le long de la hauteur et de la largeur de la section.

Soit une section transversale d'une poutre soumise à une force de cisaillement Qz=60 kN. Calculer les contraintes de cisaillement au point K de la section transversale.

La poutre librement soutenue, dont la section est représentée dans le schéma ci-dessous, est chargée d'une charge continue. Pour la section de la poutre où la force de cisaillement est la plus élevée, réalisez des graphiques de répartition des contraintes le long de la hauteur de la section.

Pour la section comme sur l'illustration, vous devez déterminer les valeurs des contraintes de flexion et de cisaillement aux points indiqués, ainsi que tracer des graphiques de ces contraintes, sachant que dans cette section, le moment de flexion M est de 5 kNm et la force de cisaillement T est de 100 kN.

Pour la section illustrée sur le schéma, déterminez les valeurs des contraintes de flexion et de cisaillement aux points marqués et tracez les graphiques de ces contraintes, sachant que dans cette section, le moment de flexion est de M = 5 kNm et la force de cisaillement est de T = 100 kN.

Une poutre d'appui unilatérale d'une section rectangulaire est soumise à une force P à une extrémité. Trouver le rapport entre les contraintes normales maximales dans la section critique et les contraintes de cisaillement maximales.

Le profilé en H soudé comme sur l'image est soumis à une force de cisaillement T=40kN. En connaissant les contraintes admissibles pour le matériau de soudure kt=80MPa, calculer : a) l'épaisseur minimale a1 des soudures, s'il s'agit de soudures continues. b) le pas t des soudures si leur épaisseur est a=5mm et leur longueur l=50mm.

Calculer /(Σ_{extr}, \tau_{extr}/).