Lista zadań
Exemple 1
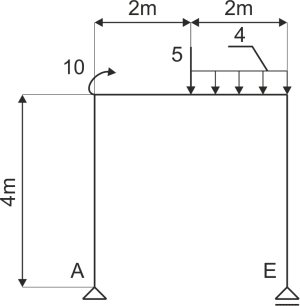
Le cadre est soutenu comme indiqué sur le dessin. Libérez le système des contraintes et écrivez les équations d'équilibre.
Exemple 2
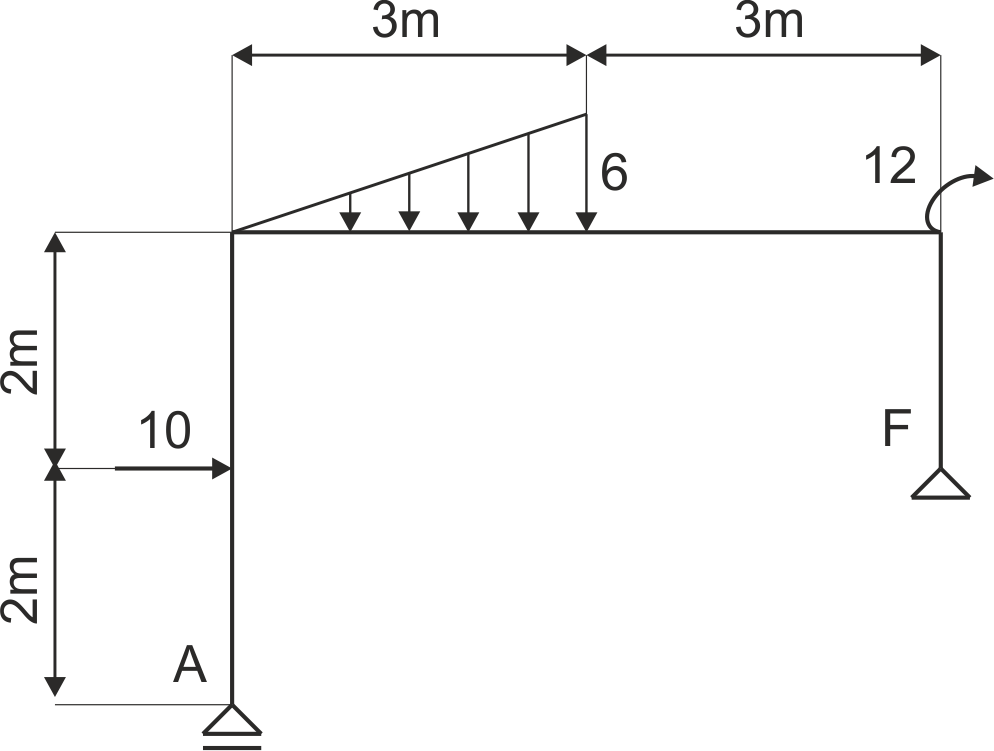
Une armature est soutenue comme sur l'illustration. Libérez le système des contraintes et écrivez les équations d'équilibre.
Exemple 3
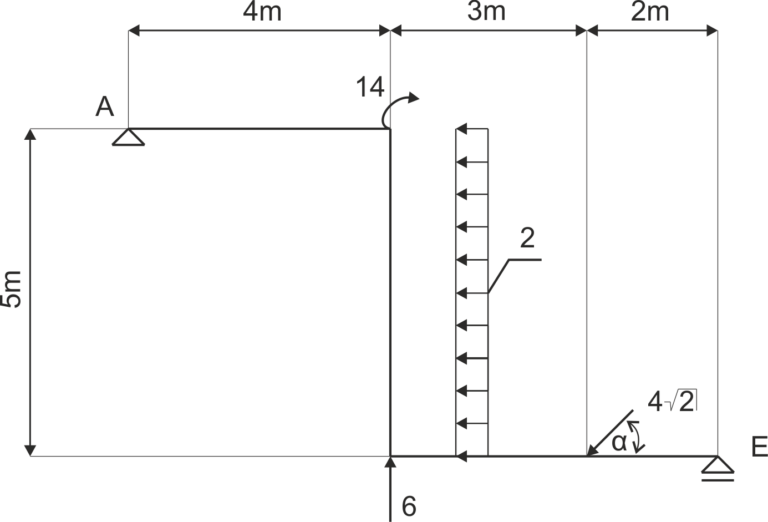
Une structure est donnée, comme illustrée sur le schéma. Libérez le système des contraintes et écrivez les équations d'équilibre. \( \alpha = 45^0 \).
Exemple 4
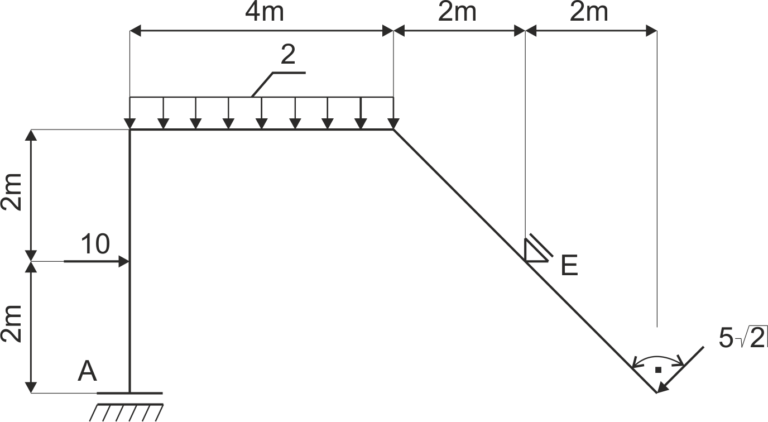
Un châssis est soutenu comme sur l'image. Libérez le système de contraintes et écrivez les équations d'équilibre.
Exemple 5
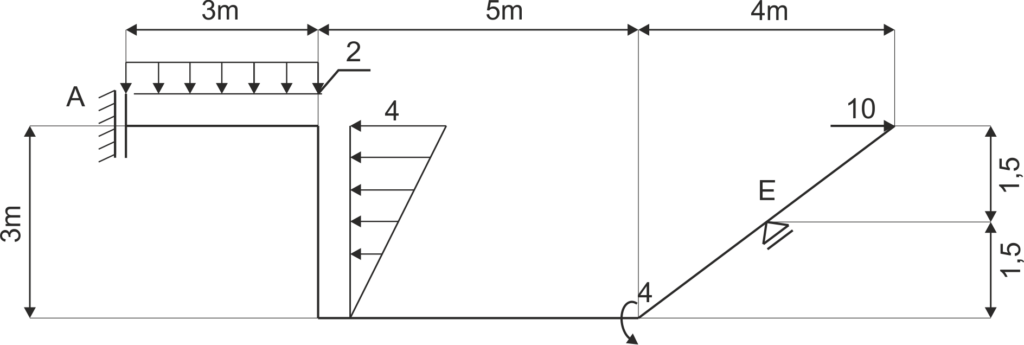
Un cadre est donné, tel qu'illustré sur le schéma. Libérez le système des contraintes et écrivez les équations d'équilibre.
Exemple 6
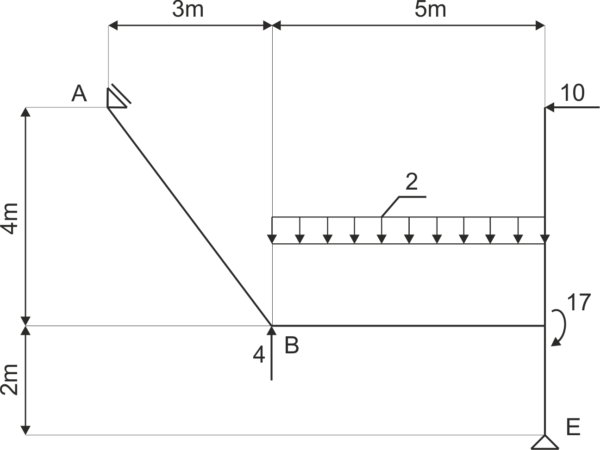
Une structure est donnée avec un support comme sur le dessin. Libérez le système des contraintes et écrivez les équations d'équilibre.
Exemple 7
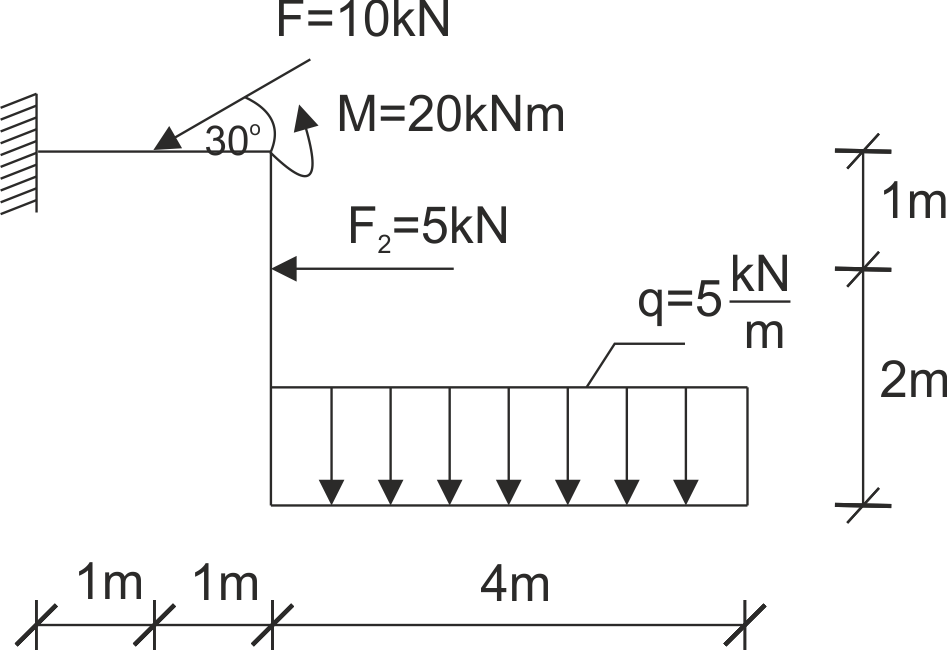
Un châssis est donné, comme sur l'illustration. Libérez le système de ses contraintes et écrivez les équations d'équilibre.
Exemple 8
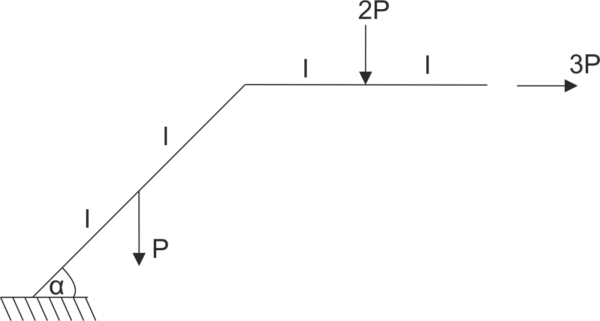
Un cadre est donné, soutenu comme sur l'image. Libérez le système des contraintes et écrivez les équations d'équilibre.
Exemple 9
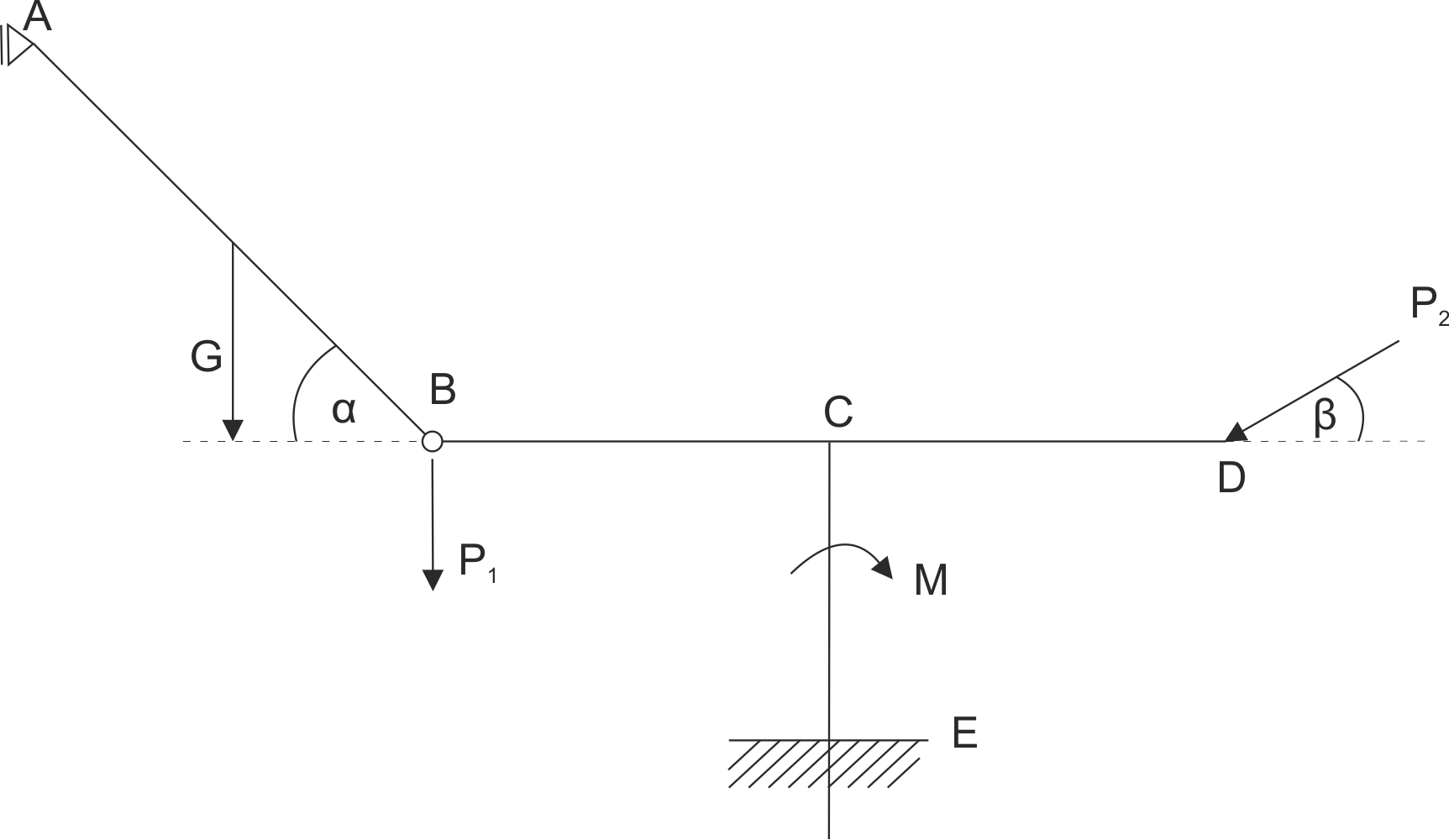
Calculer les réactions de support et les réactions dans l'articulation. Données : AB=2a, BC=CD=a, CE=b.
Exemple 10

Calculer les réactions d'appui sans diviser le système en deux parties par une articulation.
Exemple 13
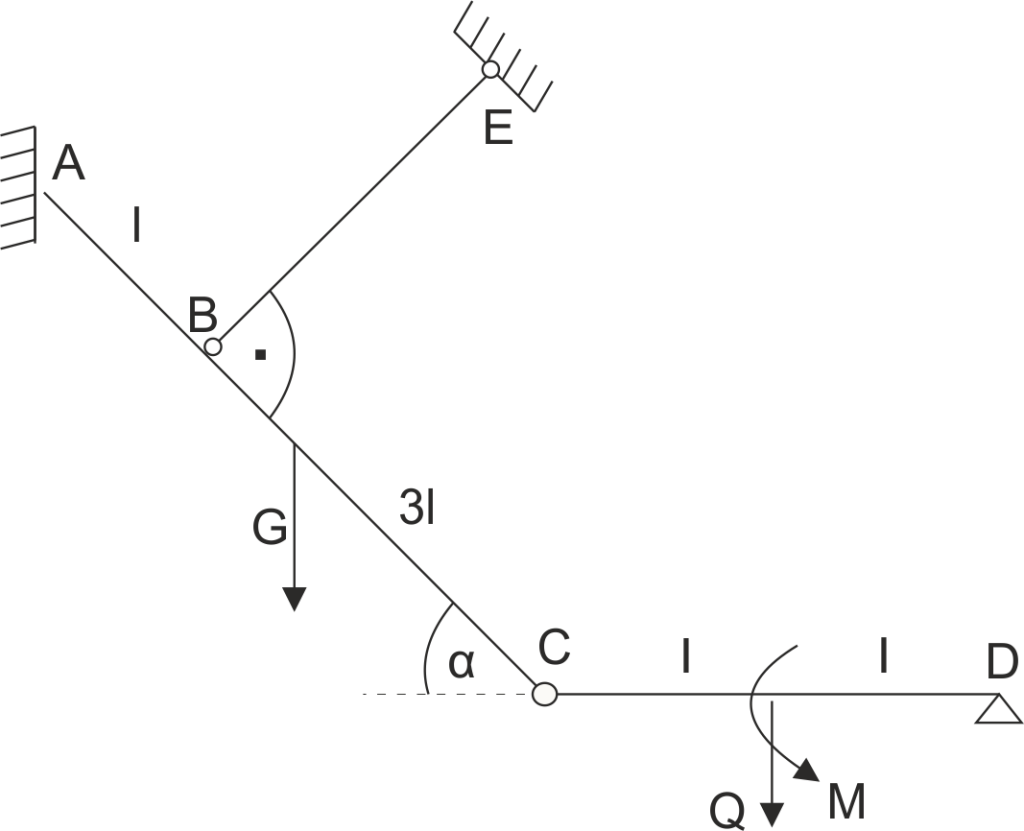
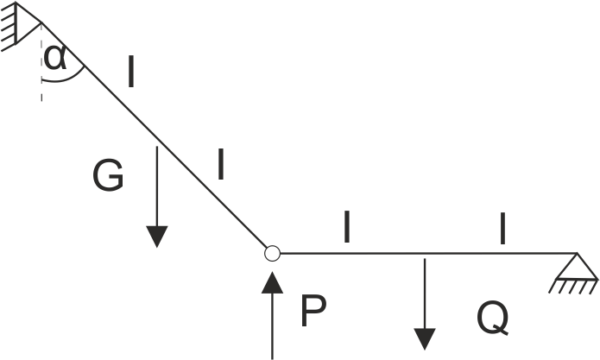
Il s'agit d'une structure poutre-poteau. La poutre AC (avec un poids G) et la poutre CD (avec un poids Q) sont reliées par une articulation. La poutre AC est supportée librement au point A et est également suspendue par une tringle BE. Calculer les réactions d'appui ainsi que les réactions d'articulation.
Exemple 14
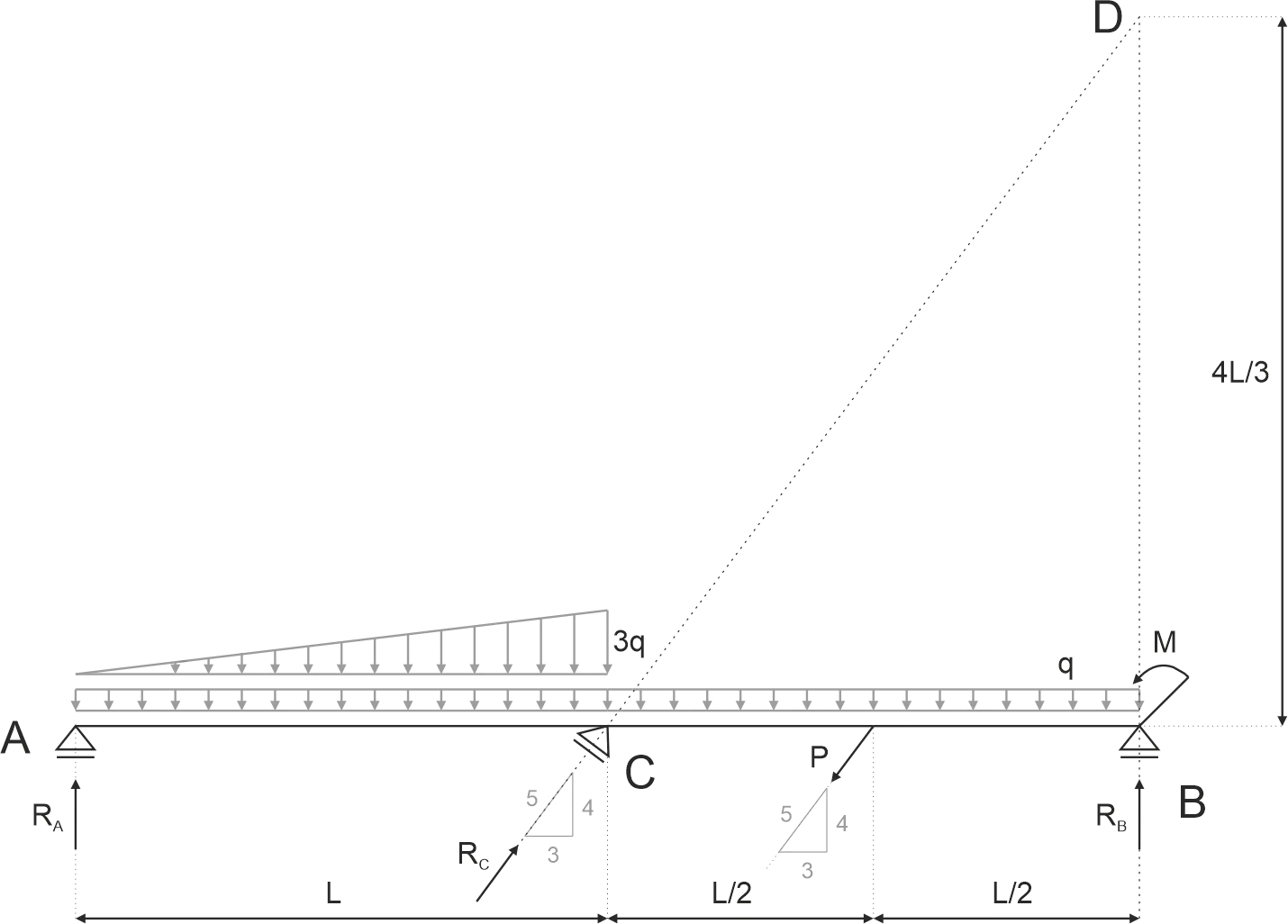
Wyznacz les valeurs des réactions \(R_A\), \(R_B\) et \(R_C\) dans la poutre illustrée sur le dessin. On considère une valeur de moment \(M=400 kNm\), une valeur de force \(P=100 kN\), une valeur de charge répartie \(q=10 kN/m\) et une longueur \(L=10 m\).