La barre diagonale est soutenue par un mur et est articulée à la barre verticale, qui est fixée. Libérez le système des contraintes et écrivez les équations d'équilibre statique.

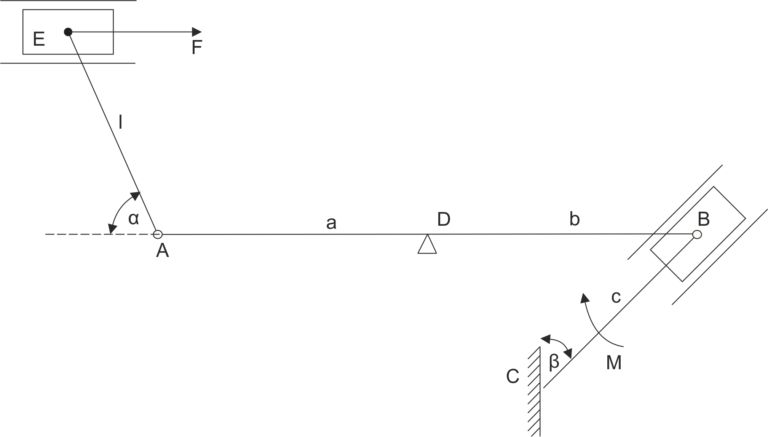
On nous donne un agencement de trois barres connectées par des articulations. La barre inférieure est soutenue librement par un support. Libérez l'agencement des contraintes et écrivez les équations d'équilibre statique.

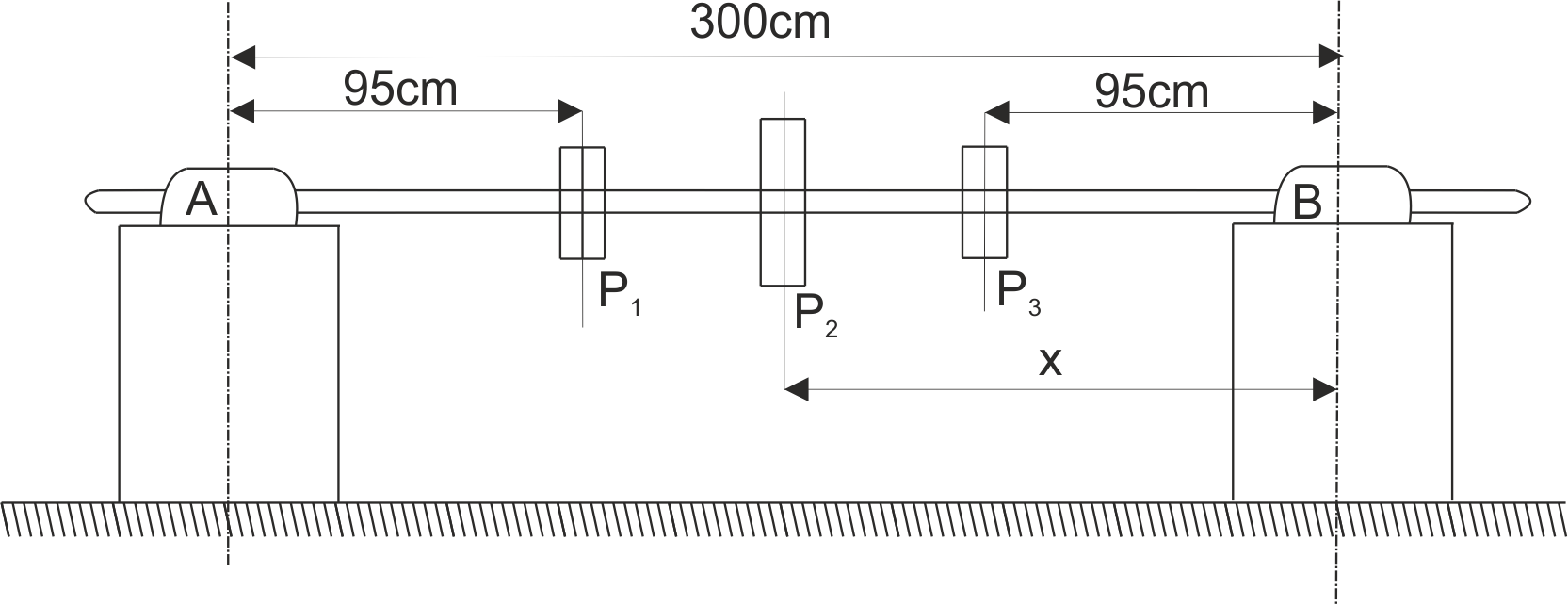
Un arbre de transmission AB a trois poulies de poids P1=3 kN, P2=5 kN, P3=2 kN. Les dimensions sont indiquées sur l'image. À quelle distance x de l'axe B faut-il fixer la poulie de poids P2 afin que les réactions des deux paliers soient égales? On néglige le poids de l'arbre.

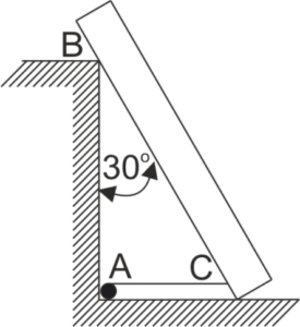
Une poutre homogène pesant 60 kg et mesurant 4 mètres, s'appuie sur le sol lisse d'un côté et sur un poteau de 3 mètres de hauteur au point B, formant un angle de \(30^o\) avec la verticale. La poutre est maintenue dans cette position par une corde AC tendue le long du sol. Déterminez la tension T dans la corde ainsi que les réactions aux points B et C.

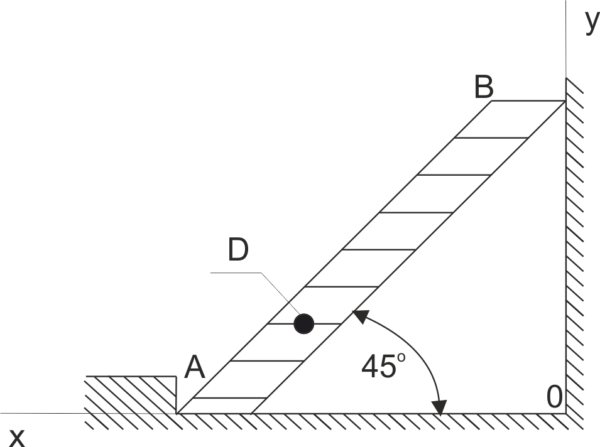
Pour un mur lisse, une échelle AB est placée, inclinée à un angle de 45^o par rapport à l'horizontale. La masse de l'échelle est de 20 kg. Au point D, situé à 1/3 de la longueur de l'échelle à partir de l'extrémité inférieure, se trouve un individu pesant 60 kg.
Calculer les forces de pression de l'échelle sur le support A et sur le mur.

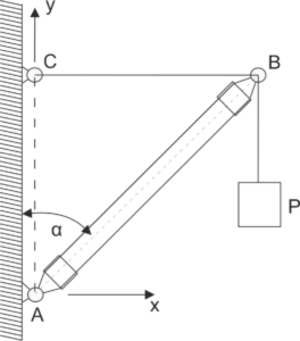
Levage est composé d'une poutre AB, dont l'extrémité inférieure est reliée par une articulation A au mur, et la partie supérieure est soutenue par un câble horizontal BC. Déterminer la tension T du câble BC et la composante verticale \(N_A\) de la force exercée sur le support A, si la charge P est égale à P=2 kN, le poids de la poutre Q=1 kN est accroché au milieu de la longueur AB, et l'angle \( \alpha=45^o \).

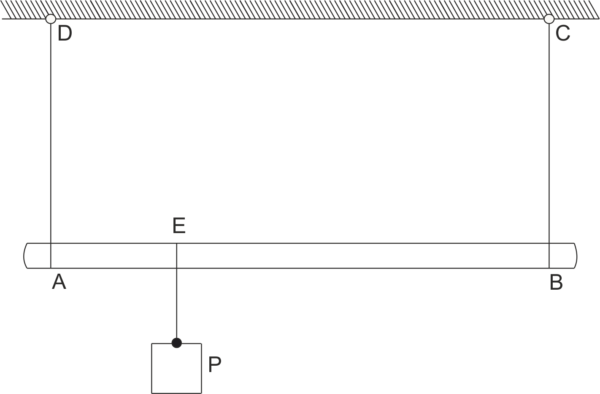
La tige homogène AB d'une longueur de 1 m et d'un poids de 20 N est suspendue horizontalement à deux câbles parallèles AC et BD. Un poids P = 120 N est suspendu au point E de la tige, à une distance de 0,25 m du point A. Calculer les forces dans les câbles \( T_{AC}, T_{BD} \).

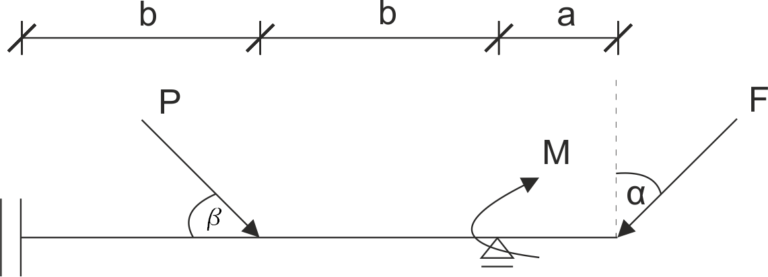
Une poutre est supportée par une patin vertical et un support coulissant articulé. Libérez le système des contraintes et enregistrez les équations d'équilibre statique.

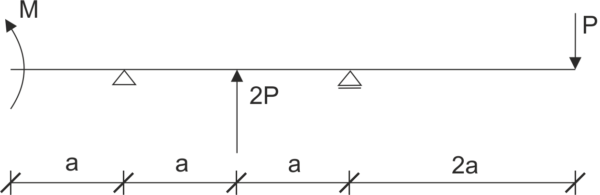
Dans la figure ci-jointe, une poutre est soutenue comme indiqué. Libérez le système des contraintes et écrivez les équations d'équilibre.

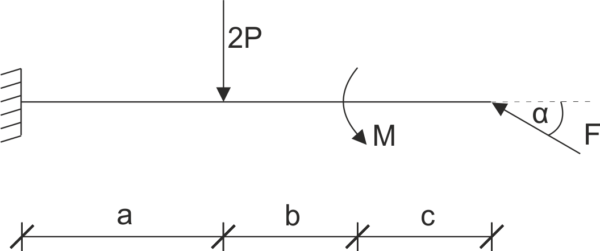
Une poutre est soutenue comme sur le dessin. Libérez le système des contraintes et écrivez les équations d'équilibre.

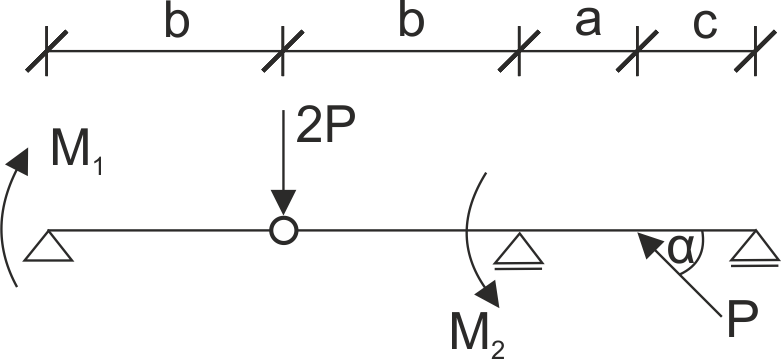
Une poutre est soutenue comme sur l'image. Libérez la structure des contraintes, divisez la poutre articulée en poutres simples et enregistrez les équations d'équilibre.

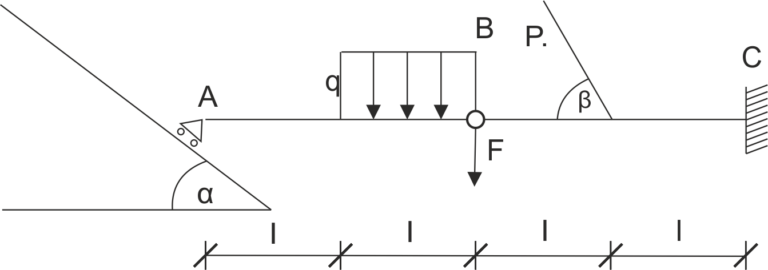
Une poutre est soutenue comme indiqué sur le schéma. Libérez le système des liaisons, divisez la poutre articulée en poutres droites et enregistrez les équations d'équilibre.