Lista zadań
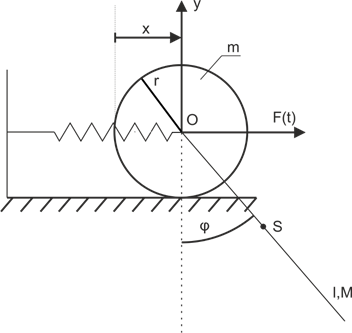
Exemple 1
En utilisant l'équation de Lagrange du deuxième type, déterminer l'équation du mouvement.
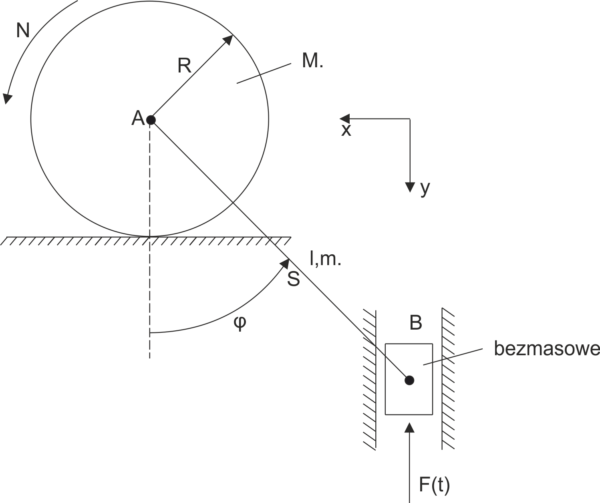
Exemple 2
En utilisant l'équation de Lagrange de la deuxième sorte, déterminez l'équation du mouvement.
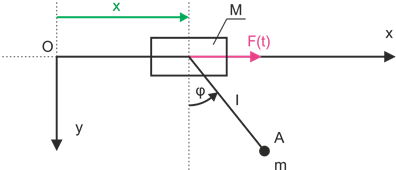
Exemple 3
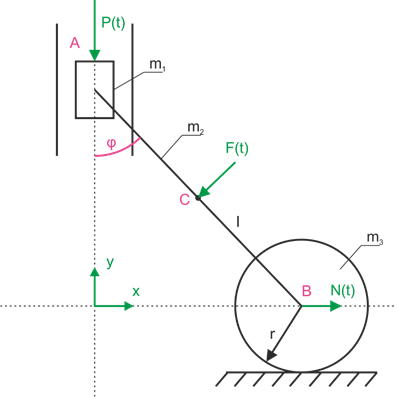
En utilisant l'équation de Lagrange de deuxième espèce pour déterminer l'équation du mouvement.
Exemple 3
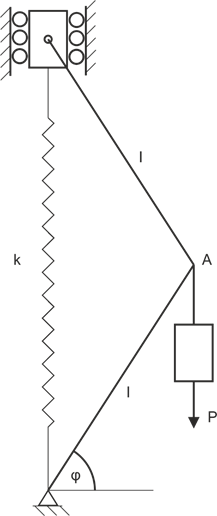
Les barres sont sans poids, la valeur de la force de gravité suspendue \(P=k\cdot l\), le ressort n'est pas déformé pour \(\varphi={30}^o\). Trouvez les positions d'équilibre et étudiez leur stabilité.
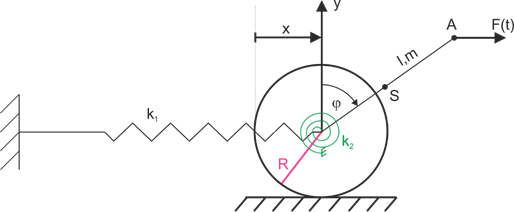
Exemple 4
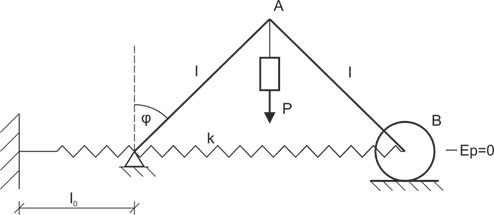
Pour \(\varphi=0\), le ressort n'est pas déformé. Déterminez les positions d'équilibre et étudiez leur stabilité. Nous négligeons les masses des barres, le ressort est linéaire. \(P=kl\).
Exemple 4

En utilisant l'équation de Lagrange de deuxième espèce, déterminez l'équation du mouvement.
Exemple 6
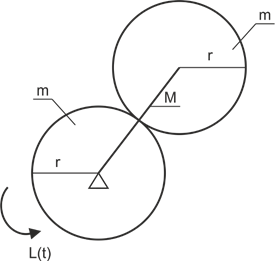
Utilisez l'équation de Lagrange de deuxième espèce pour trouver l'équation du mouvement.
Exemple 7
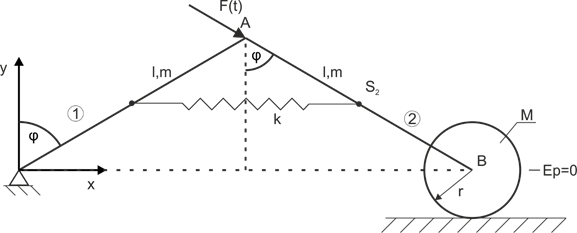
En utilisant l'équation de Lagrange de deuxième espèce, déterminons l'équation du mouvement.
Exemple 8
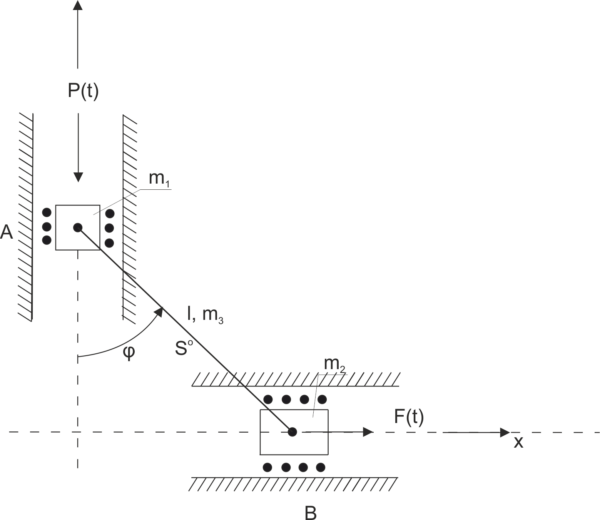
En utilisant l'équation de Lagrange de deuxième espèce, déterminer l'équation du mouvement.
Exemple 10
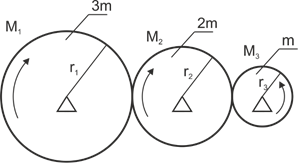
En utilisant l'équation de Lagrange de deuxième espèce pour déterminer l'équation du mouvement.