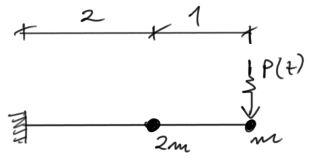
Pour la poutre donnée, déterminez les fréquences propres de vibration et tracez leurs formes. Vérifiez la condition d'orthogonalité. Tracez les moments finaux résultant des forces d'inertie (en prenant la fréquence d'excitation comme la moyenne arithmétique des fréquences propres calculées précédemment, c'est-à-dire \( \theta=\frac{\omega_1+\omega_2}{2} \) ). \( \text{Données :} \ EI= 2,1\cdot 10^5 \ kNm^2, \ m=200 \ kg, \ P=10\cdot sin(\theta \ t) \)

Pour le cadre donné, calculer les forces d'inertie. \( \text{Données :} \ EI= 4000 \ kNm^2, \ m=700 \ kg, \ P=25 sin(pt), \ p=15\ \frac{rad}{s} \)

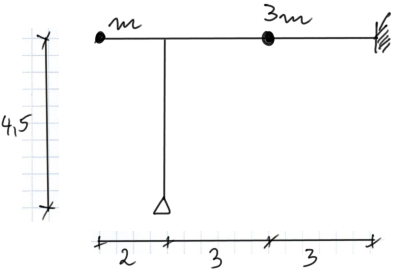
Pour la section donnée, tracer les moments ultimes provenant des forces d'inertie. Tracez les enveloppes des moments. Données : \( \mathrm{E}=2.1 \cdot 10^{11} \frac{\mathrm{N}}{\mathrm{m}^2}, \mathrm{~m}=660 \mathrm{~kg}, \mathrm{~m}_{\mathrm{w}}=2250 \mathrm{~kg}, \mathrm{e}=4.3 \mathrm{~mm}, \mathrm{n}=470 \frac{\mathrm{tr/min}}{\mathrm{min}} \), section de poutrelle IPN 200.

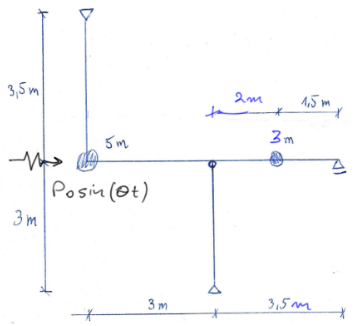
Pour le cadre donné, tracer les moments ultimes provenant des forces d'inertie. Dessiner les enveloppes des moments. Données : \( \mathrm{E}=2,1 \cdot 10^{11} \frac{\mathrm{N}}{\mathrm{m}^2}, \mathrm{~m}=680 \mathrm{~kg}, \mathrm{~m}_{\mathrm{w}}=400 \mathrm{~kg}, \mathrm{e}=2 \mathrm{~mm}, \mathrm{n}=300 \frac{\mathrm{obr}}{\mathrm{min}} \), section du cadre avec un moment d'inertie \(I=4250\ cm^4 \).

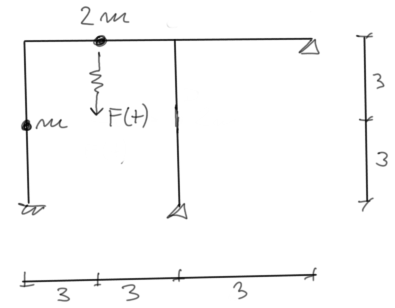
Pour le cadre donné, dessinez les moments ultimes résultant des forces d'inertie. Données : \( \theta =0,8\cdot \omega_1 \, F_0=2\ kN \)

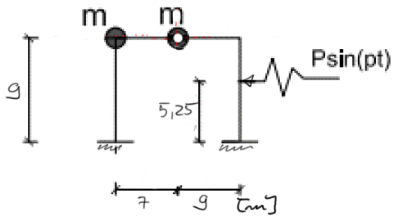
Pour le cadre donné, dessinez les moments finaux provenant des forces d'inertie. Vérifiez si les contraintes dans la barre de section rectangulaire de 12 x 24 cm et de module de Young de 210 GPa ne dépassent pas la résistance admissible de 240 MPa. Données : \( \mathrm{p}=8.25 \frac{\mathrm{rad}}{\mathrm{s}}, \mathrm{m}=2.75 \mathrm{t}, \mathrm{P}=20.5 \mathrm{kN} \)