Diagramas en Vigas
En este texto aprenderás qué es una fuerza axial (normal), una fuerza cortante y un momento flector, así como la convención de signos de estas fuerzas internas.
Describiremos cuáles son las relaciones entre la carga distribuida, la fuerza cortante y el momento flector, y qué cambios en los diagramas de fuerzas internas debemos esperar para una carga determinada en la viga.
A continuación, se muestra la convención habitual de signos para cada fuerza interna:

1. Fuerza normal (N)
2. Fuerza cortante (Q)
3. Momento flector (M)
Relación entre:
Puede ser constante o variar según la posición x en la viga.
\( \frac{dQ(x)}{dx} = -q(x) \)
Dicho de otro modo, el cambio en la fuerza cortante a lo largo de la viga está causado por la carga distribuida.
\( \frac{dM(x)}{dx} = Q(x) \)
Por lo tanto, el cambio en el momento flector a lo largo de la viga se debe a la fuerza cortante.
1) El método básico para trazar diagramas de fuerzas internas consiste en escribir inicialmente las funciones de fuerzas internas. En nuestros cursos, incluyendo materiales gratuitos, encontrarás ejemplos de cómo resolver una viga de principio a fin usando este método.
2) Un método más avanzado consiste en trazar los diagramas sin anotar las funciones de fuerzas internas, y para este método es útil conocer ciertas reglas para trazar los diagramas de fuerzas internas:
3) Una relación interesante entre Q(x) y M(x), a saber, que el cambio en el diagrama de momento flector corresponde al área bajo el diagrama de la fuerza cortante, también se puede usar para trazar diagramas. Encontrarás cálculos que usan este método en nuestro material de YouTube; sin embargo, es un método que se muestra raramente en clase.
La teoría es útil, pero entenderás mejor todo al resolver ejemplos:
Curso en vídeo que muestra cómo determinar saltos en los diagramas
Describiremos cuáles son las relaciones entre la carga distribuida, la fuerza cortante y el momento flector, y qué cambios en los diagramas de fuerzas internas debemos esperar para una carga determinada en la viga.
Cálculo de vigas
Tipos de fuerzas internas
Existen tres tipos básicos de fuerzas internas que pueden aparecer en las vigas:
1. Fuerzas normales (axiales) – surgen de la acción de fuerzas a lo largo del eje de la viga. Si la fuerza se dirige a lo largo del eje de la viga, provocando tracción o compresión, se trata de una fuerza normal. Se denota como N.
2. Fuerzas cortantes – actúan perpendicularmente al eje de la viga y generan esfuerzos cortantes internos. Se denotan como Q y son responsables del desplazamiento vertical de las diferentes secciones transversales de la viga entre sí.
3. Momento flector – es el momento de la fuerza que causa la flexión de la viga. Afecta la curvatura de la viga y varía a lo largo de su longitud. El momento flector se denota como M.
2. Fuerzas cortantes – actúan perpendicularmente al eje de la viga y generan esfuerzos cortantes internos. Se denotan como Q y son responsables del desplazamiento vertical de las diferentes secciones transversales de la viga entre sí.
3. Momento flector – es el momento de la fuerza que causa la flexión de la viga. Afecta la curvatura de la viga y varía a lo largo de su longitud. El momento flector se denota como M.
Convención de signos para las fuerzas internas
La convención de signos para las fuerzas internas en la mecánica de vigas es clave para interpretar correctamente sus direcciones y magnitudes, así como para anotar los resultados de manera coherente en el análisis estructural.A continuación, se muestra la convención habitual de signos para cada fuerza interna:

Fig. 1. Convención de signos para las fuerzas internas
1. Fuerza normal (N)
- Tracción: Una fuerza que estira la viga (actúa hacia afuera de la sección, “alejándose” del centro de la viga) suele considerarse positiva. En resumen: si la viga se tracciona, la fuerza normal N es positiva.
- Compresión: Una fuerza que comprime la viga (actúa en dirección axial hacia dentro de la sección, provocando compresión) se considera negativa.
- Compresión: Una fuerza que comprime la viga (actúa en dirección axial hacia dentro de la sección, provocando compresión) se considera negativa.
2. Fuerza cortante (Q)
- Fuerza cortante positiva: Cuando la fuerza actúa hacia arriba en el lado izquierdo de la sección o hacia abajo en el lado derecho de la sección, la fuerza cortante se considera positiva.
- Fuerza cortante negativa: La fuerza que actúa hacia abajo en el lado izquierdo de la sección o hacia arriba en el lado derecho de la sección se considera negativa.
- Fuerza cortante negativa: La fuerza que actúa hacia abajo en el lado izquierdo de la sección o hacia arriba en el lado derecho de la sección se considera negativa.
3. Momento flector (M)
- Momento flector positivo (momento que causa una “sonrisa”): Si el momento flector hace que la viga se doble en una forma similar a una “sonrisa” (es decir, las fibras superiores de la viga están comprimidas y las inferiores traccionadas), el momento es positivo.
- Momento flector negativo (momento que causa una “mueca triste”): Cuando la viga se dobla en sentido contrario (las fibras superiores traccionadas y las inferiores comprimidas — una “mueca triste”), el momento flector es negativo.
- Momento flector negativo (momento que causa una “mueca triste”): Cuando la viga se dobla en sentido contrario (las fibras superiores traccionadas y las inferiores comprimidas — una “mueca triste”), el momento flector es negativo.
Relación entre:
carga distribuida <-> fuerza cortante <-> momento flector
1. Carga distribuida q(x)
La carga distribuida q(x) es una fuerza repartida a lo largo de la viga que actúa por unidad de longitud.Puede ser constante o variar según la posición x en la viga.
2. Fuerza cortante Q(x)
La relación entre la carga distribuida y la fuerza cortante es:\( \frac{dQ(x)}{dx} = -q(x) \)
Dicho de otro modo, el cambio en la fuerza cortante a lo largo de la viga está causado por la carga distribuida.
- Cuando la carga distribuida q(x) es positiva (p.ej., dirigida hacia abajo), la fuerza cortante Q(x) disminuye a lo largo de la viga.
- Cuando q(x) = 0 (no hay carga), la fuerza cortante es constante.
- Si la fuerza cortante es cero, entonces el momento flector es constante.
- Cuando q(x) = 0 (no hay carga), la fuerza cortante es constante.
- Si la fuerza cortante es cero, entonces el momento flector es constante.
3. Momento flector M(x)
La relación entre la fuerza cortante y el momento flector es:\( \frac{dM(x)}{dx} = Q(x) \)
Por lo tanto, el cambio en el momento flector a lo largo de la viga se debe a la fuerza cortante.
- Cuando la fuerza cortante Q(x) es positiva, el momento flector M(x) aumenta.
- Cuando en el diagrama de fuerza cortante Q(x) = 0, el momento flector alcanza un extremo.
- Cuando en el diagrama de fuerza cortante Q(x) = 0, el momento flector alcanza un extremo.

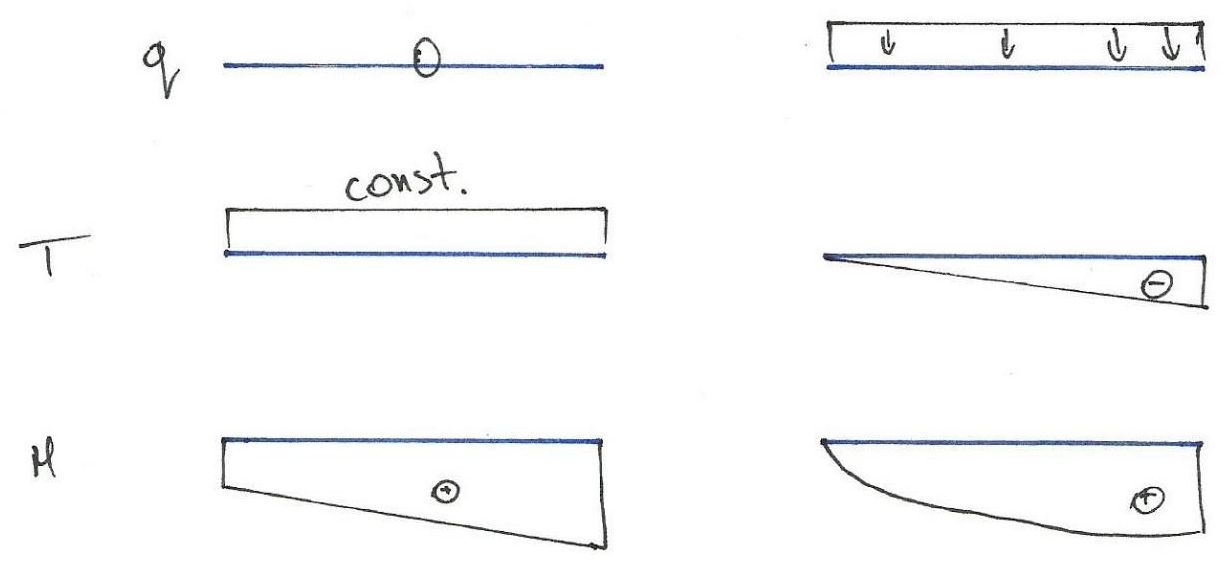
Fig. 2. Relación: carga distribuida – fuerza cortante – momento flector
Reglas para trazar los diagramas de fuerzas internas
Supongamos que hay tres métodos para trazar los diagramas de fuerzas internas:1) El método básico para trazar diagramas de fuerzas internas consiste en escribir inicialmente las funciones de fuerzas internas. En nuestros cursos, incluyendo materiales gratuitos, encontrarás ejemplos de cómo resolver una viga de principio a fin usando este método.
2) Un método más avanzado consiste en trazar los diagramas sin anotar las funciones de fuerzas internas, y para este método es útil conocer ciertas reglas para trazar los diagramas de fuerzas internas:
- Si en cualquier punto de la viga se aplica una fuerza transversal, en el diagrama de fuerza cortante Q se produce un salto igual al valor de dicha fuerza,
el salto se produce en la dirección de la fuerza al leer el diagrama de izquierda a derecha,
- Si en un tramo de la viga existe una carga distribuida, en el diagrama de fuerza cortante Q en ese tramo hay un cambio igual a la resultante de la carga distribuida,
con la dirección coherente con la resultante (al leer de izquierda a derecha),
- Si en cualquier punto de la viga se aplica un momento concentrado, en el diagrama de momentos M se produce un salto igual al valor de dicho momento,
siendo el salto positivo o negativo según sea horario o antihorario — véase la convención de signos.
el salto se produce en la dirección de la fuerza al leer el diagrama de izquierda a derecha,
- Si en un tramo de la viga existe una carga distribuida, en el diagrama de fuerza cortante Q en ese tramo hay un cambio igual a la resultante de la carga distribuida,
con la dirección coherente con la resultante (al leer de izquierda a derecha),
- Si en cualquier punto de la viga se aplica un momento concentrado, en el diagrama de momentos M se produce un salto igual al valor de dicho momento,
siendo el salto positivo o negativo según sea horario o antihorario — véase la convención de signos.

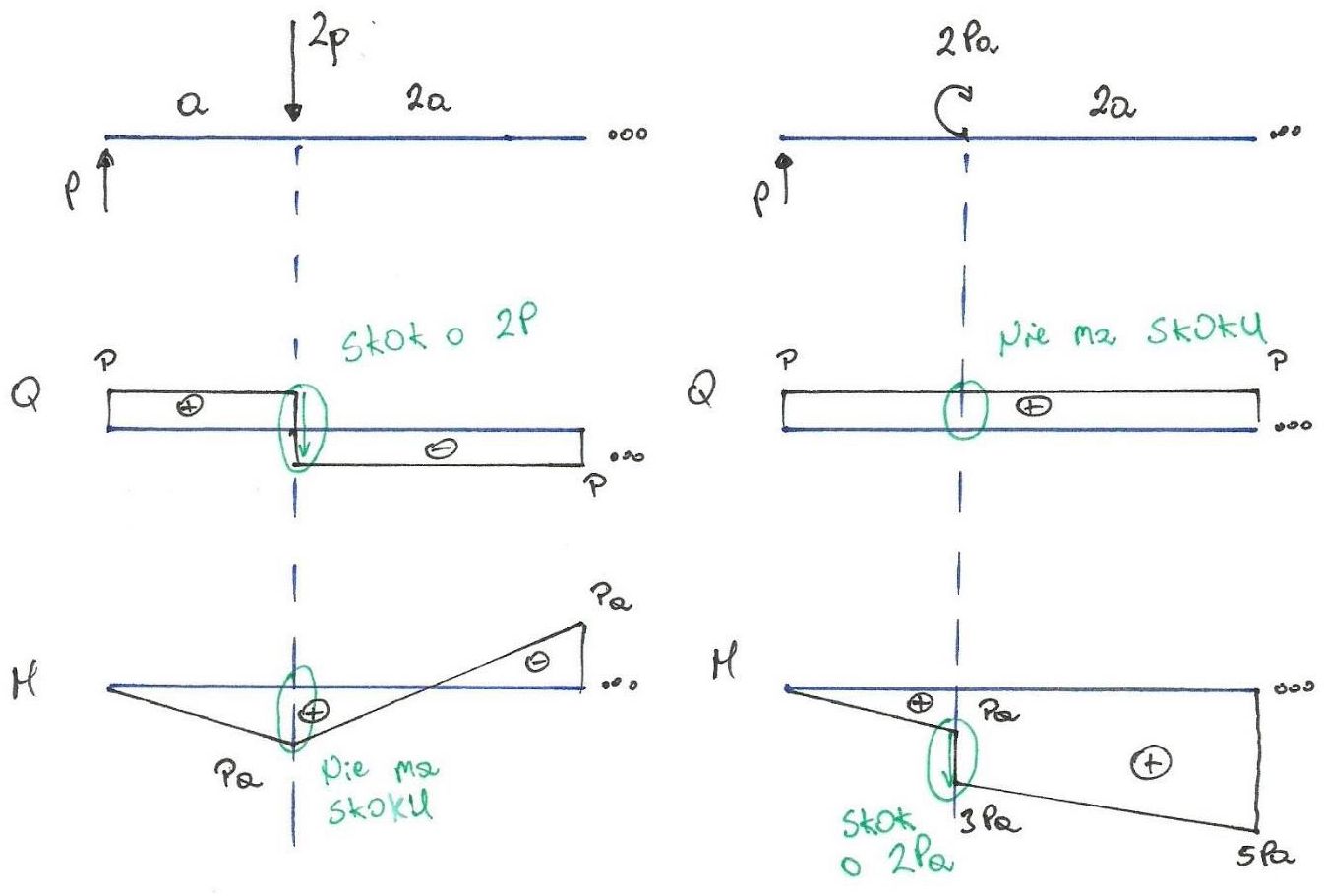
Fig. 3. Carga en la viga y saltos en los diagramas Q y M
3) Una relación interesante entre Q(x) y M(x), a saber, que el cambio en el diagrama de momento flector corresponde al área bajo el diagrama de la fuerza cortante, también se puede usar para trazar diagramas. Encontrarás cálculos que usan este método en nuestro material de YouTube; sin embargo, es un método que se muestra raramente en clase.
La teoría es útil, pero entenderás mejor todo al resolver ejemplos:
Curso en vídeo que muestra cómo determinar saltos en los diagramas
y describe los métodos 2) y 3) para trazar diagramas con 4 ejemplos.
Conjunto de 19 vigas con soluciones breves
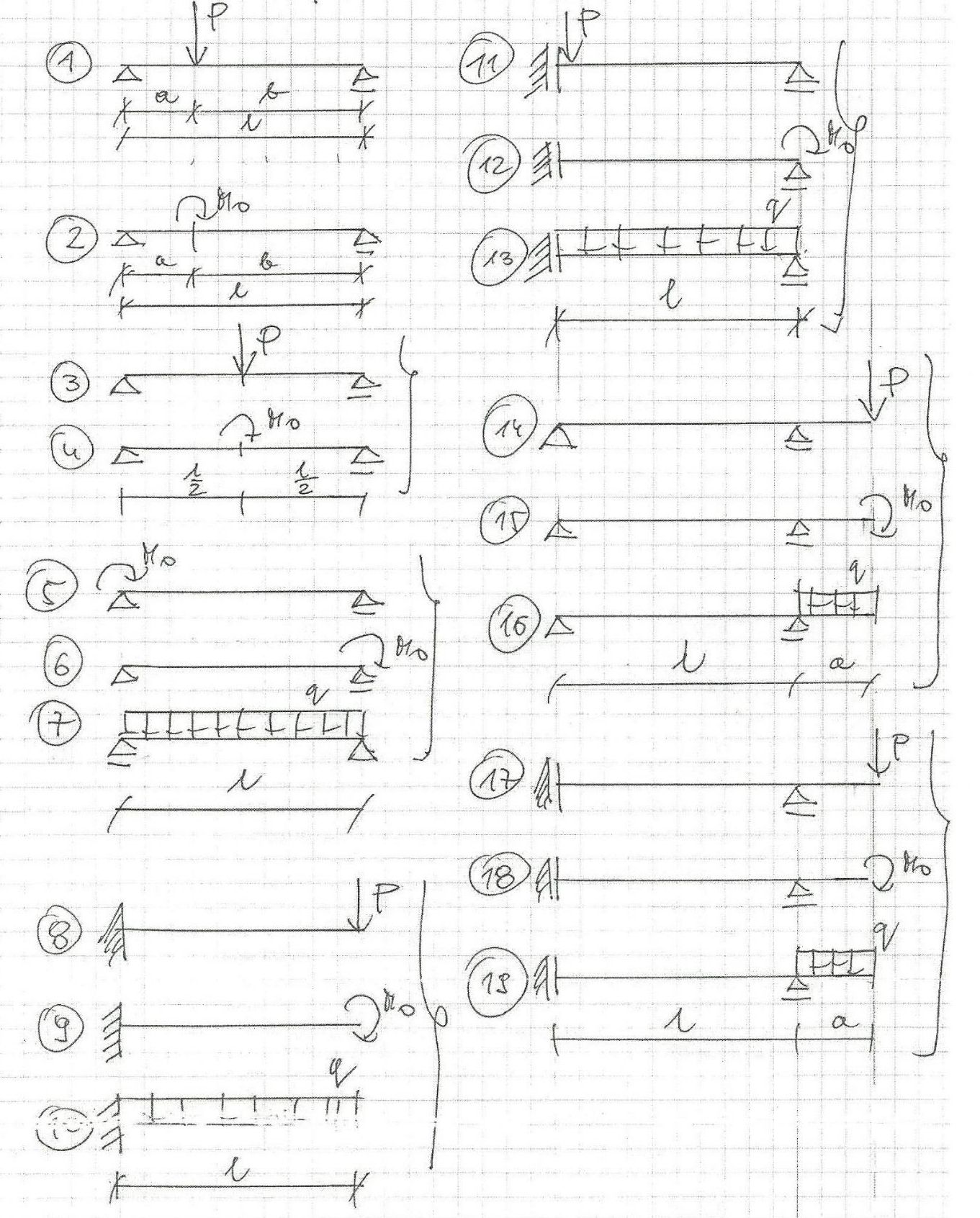
A continuación se presentan soluciones breves + diagramas para cada viga
Soluciones












A continuación también encontrarás enlaces a numerosos ejemplos de solución para vigas rectas, inclinadas y articuladas.