Tipos de apoyos en un plano y en el espacio 3D

¿Qué es un apoyo en la mecánica de estructuras?

Un apoyo en la mecánica de estructuras es un elemento que proporciona una reacción a las fuerzas y momentos que actúan sobre una estructura. En el contexto de la ingeniería y el diseño estructural, los apoyos son componentes esenciales que permiten la transferencia de cargas, garantizan la estabilidad y el equilibrio de la estructura y facilitan su funcionamiento de manera segura y eficiente.

El número de movimientos independientes que un objeto puede realizar en un plano

Los diferentes tipos de apoyos restringen distintas posibilidades de movimiento en un plano o en el espacio.
En un plano existen tres principales grados de libertad de movimiento:

• Translación a lo largo del eje X: Es el movimiento a lo largo del eje X horizontal, que permite al objeto desplazarse en el plano hacia la izquierda o la derecha.

• Translación a lo largo del eje Y: Es el movimiento a lo largo del eje Y vertical, que permite al objeto desplazarse hacia arriba o hacia abajo en el plano.

• Rotación alrededor del eje vertical (Z): Es el giro del objeto alrededor de un eje perpendicular al plano, generalmente denominado eje Z. Este movimiento permite que el objeto gire alrededor del centro del plano.

Cabe señalar que los grados de libertad pueden variar según el contexto y las características específicas de la construcción. Por ejemplo, un mecanismo complejo puede incluir movimientos adicionales, como inclinación o rotación alrededor de otros ejes.
En el análisis del movimiento de objetos en un plano, estos tres grados de libertad básicos constituyen un punto de referencia clave.

Tipos de apoyos en un plano

Dado que en un plano tenemos tres grados de libertad de movimiento, los apoyos pueden eliminar estos grados de libertad en diferentes combinaciones. Quitar mediante un apoyo la posibilidad de movimiento (por ejemplo, horizontal) conlleva la aparición en el apoyo de una reacción en dicha dirección. Primero caracterizaremos brevemente los tipos de apoyos en el plano y luego, para mayor claridad, los resumiremos en una tabla con la siguiente información sobre los apoyos en un plano:
- nombre(s) común(es),
- símbolo(s) gráfico(s),
- qué tipo de reacción se presenta,
- qué grado de libertad de movimiento se elimina.

a) apoyo articulado deslizante

Bloquea la posibilidad de movimiento lineal en una dirección, permite el movimiento en la dirección perpendicular a la bloqueada y también permite la rotación. Las representaciones gráficas que podemos encontrar en la literatura son:

Fig.1. Apoyo articulado deslizante

La línea horizontal bajo el símbolo triangular del apoyo articulado muestra en qué dirección es posible el movimiento. Está bloqueada la dirección perpendicular a dicha posibilidad de movimiento y en esa dirección aparece la reacción. Por supuesto, el apoyo articulado deslizante puede usarse en diferentes ángulos, como se muestra a continuación:

Fig.2. Apoyo articulado deslizante en diferentes ángulos con la reacción indicada

Si el apoyo y la reacción se encuentran en ángulo, a menudo para simplificar los cálculos es más conveniente descomponer esa reacción en sus componentes:

Fig.3. Descomposición de la reacción en componentes

Tras la descomposición en componentes, en los cálculos utilizamos o bien la reacción resultante (roja) o bien ambas componentes (azules) – nunca las dos opciones a la vez. Es decir, al escribir ecuaciones de equilibrio o determinar fuerzas internas, utilizamos o las componentes o la resultante, pero no ambas simultáneamente.

b) apoyo articulado no deslizante

En el apoyo articulado no deslizante también existe en realidad una sola reacción, sin embargo, no conocemos su dirección. Por ello, lo mejor es marcar de inmediato dos componentes de esa reacción. No tienen que ser necesariamente vertical y horizontal, pero deben ser perpendiculares entre sí. También es importante señalar que el sentido de las reacciones nunca es determinante, y es solo una cuestión de nuestra suposición. En la siguiente figura, además del símbolo del apoyo, se muestra una barra saliendo del mismo (por supuesto, no importa en qué ángulo salga dicha barra)

Fig.4. Apoyo articulado no deslizante

¡Atención! Si la barra que sale del apoyo además termina en un articulación del otro lado, entonces estamos ante un tirante/barra de celosía/cable, sobre el cual encontrarás más información más abajo.

A menudo surge la duda sobre cómo marcar las reacciones cuando vemos un apoyo no deslizante girado en un ángulo diferente. Hay que recordar que en dicho apoyo siempre hay dos reacciones perpendiculares entre sí y depende de nosotros en qué direcciones las marquemos. Cada uno de los variantes mostrados a continuación está bien.

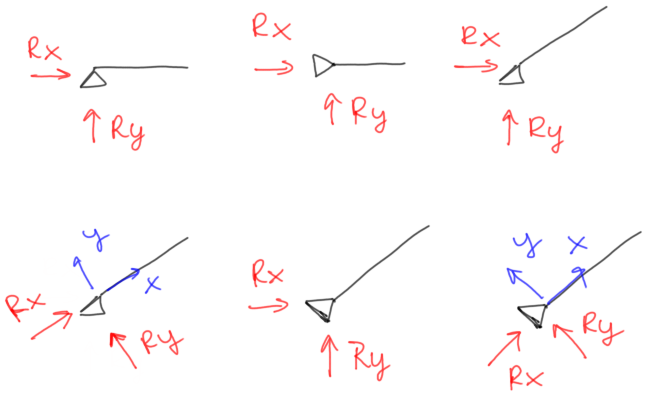
Fig.5. Apoyo articulado no deslizante con reacciones indicadas

c) barra de celosía/tirante/cable

Podemos encontrarnos, por ejemplo, con una viga/pórtico apoyado con un apoyo articulado no deslizante + un cable (Ver ejemplo gratuito 1)

Fig.6. Sistema de pórtico soportado por un cable

o con una viga soportada solo con cables (Ver ejemplo gratuito 2)

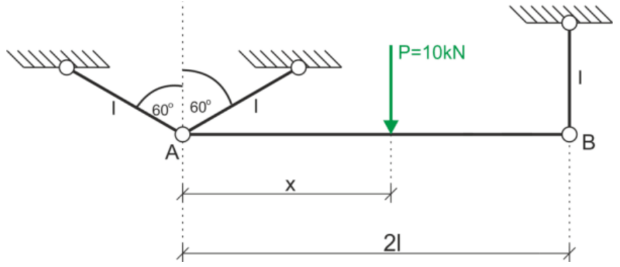
Fig.7. Viga soportada por tres tirantes

Para que hablemos de un cable/tirante/barra de celosía se deben cumplir las siguientes condiciones:

- La barra debe estar articulada en ambos extremos (estos son los nodos de la barra),
- La barra debe ser lineal (no puede tener quiebres, ver ejemplo abajo),
- No puede haber carga entre nodos,
- La carga puede, como máximo, aplicarse en un nodo (recordemos que si es un momento concentrado, no puede aplicarse estrictamente en la articulación, debe aplicarse en un lado u otro de la misma)

Una barra de celosía se caracteriza principalmente por:

- sólo presenta fuerza axial (normal),
- no presenta fuerzas cortantes ni momentos flectores.

A continuación, a la izquierda un ejemplo de dos barras de celosía, a la derecha debido a la falta de articulación en el centro, la barra no es lineal, por lo tanto, no es una barra de celosía, sino un sistema de pórtico apoyado en dos apoyos articulados no deslizantes.

Fig.8. Ejemplo de clasificación de barra de celosía y sistema de pórtico

Esta es una diferencia fundamental entre estas dos construcciones, y se calculan de manera completamente distinta. En los apoyos articulados mostramos las reacciones como se indicó anteriormente, mientras que, en cuanto a las reacciones en una barra de celosía, tenemos dos formas de mostrarlas:

1. Cortar la barra y mostrar las fuerzas internas (axiales) en la barra y descartar la parte externa de la estructura.
2. Mostrar la reacción en el extremo de la barra, hacia afuera de la construcción, es decir, en el apoyo; la reacción se presenta sólo en el eje de la barra.

Fig.9. Segundo variante de la reacción en la barra de celosía y reacciones en un sistema de pórtico articulado.

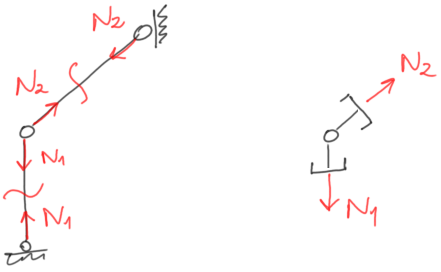
Fig.10. Primer variante de marcación de reacciones/fuerzas en la barra de celosía

En nuestra página generalmente encontrarás el primer variante, porque nos parece mejor.
En el ejemplo anterior:

a) cortamos la barra,
b) mostramos las fuerzas en la barra (siempre o hacia dentro o hacia fuera – lo mejor es asumir como arriba, hacia dentro, asumiendo que la barra se encuentra traccionada),
c) descartamos las partes externas a la construcción.

Para este ejemplo, esta operación reduce el sistema al equilibrio del nudo.

d) empotramiento completo/ménsula

El empotramiento completo, es decir, el apoyo fijo típico, elimina todas las posibilidades de movimiento en el plano, es decir, el movimiento lineal y la rotación. Por lo tanto, en él aparecen tres reacciones: dos fuerzas concentradas perpendiculares entre sí y un momento flector concentrado. Al igual que en el caso del apoyo articulado no deslizante, la dirección y el sentido de las reacciones son cuestión de nuestro supuesto (recordando únicamente que las reacciones deben ser perpendiculares entre sí).

Fig.11. Formas de marcar un empotramiento completo y sus reacciones

e) empotramiento con deslizamiento/patín

El empotramiento con deslizamiento permite el movimiento lineal en una dirección, bloqueando al mismo tiempo el movimiento lineal en la dirección perpendicular y la rotación. Podemos distinguir patines verticales y horizontales, pero el empotramiento con deslizamiento puede estar bajo cualquier ángulo. A continuación, se muestran varias posibilidades de marcación del patín junto con las reacciones en él.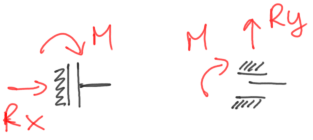

Fig.12. Patín vertical y horizontal con sus reacciones

Fig.13. Otras posibilidades de empotramiento con deslizamiento con sus reacciones

f) bloqueo de rotación/cuña

Se trata de un tipo de apoyo que se encuentra muy raramente y generalmente no se muestra estrictamente en la temática de un ejercicio típico, pero podemos encontrarnos con él al resolver una viga/pórtico mediante el método de trabajos virtuales y, por supuesto, aparece casi en cada problema del campo de la mecánica de estructuras – métodos de desplazamientos.

El bloqueo de rotación es una restricción que, como su nombre lo indica, bloquea únicamente la posibilidad de rotación del punto (nudo). Podemos encontrarnos con las siguientes representaciones del bloqueo de rotación:

Fig.14. Representación gráfica del apoyo/restricción – bloqueo de rotación

En este apoyo sólo aparece una reacción en forma de momento flector. El nudo tiene libertad de moverse en cualquier dirección, pero no puede rotar, es decir, la forma del nudo tras el desplazamiento debe seguir siendo igual que antes del desplazamiento. La primera representación a la izquierda recuerda a una cuña, y con este nombre también podemos encontrarnos. La tercera representación recuerda un patín tanto vertical como horizontal al mismo tiempo.

Grados de libertad del movimiento en el espacio 3D

En el espacio tridimensional (3D) existen seis grados de libertad de movimiento principales que definen el número de movimientos independientes que puede realizar un objeto. Estos grados de libertad son:

• Translación a lo largo del eje X,

• Translación a lo largo del eje Y,

• Translación a lo largo del eje Z,

• Rotación alrededor del eje X,

• Rotación alrededor del eje Y,

• Rotación alrededor del eje Z.

Todos estos grados de libertad en conjunto definen cómo un objeto puede moverse y girar en el espacio 3D. Gracias a esta clasificación, los ingenieros y diseñadores pueden analizar y modelar los movimientos de objetos y estructuras en tres dimensiones.

Tipos de apoyos en el espacio 3D

En un sistema plano, teniendo 3 grados de libertad de movimiento (translación en X, translación en Y, rotación en Z), logramos identificar 6 tipos de apoyos según las combinaciones de grados de libertad que dichos apoyos eliminan.
Será difícil realizar una clasificación similar de apoyos en el espacio 3D, por lo que a continuación daremos más bien principios generales sobre los apoyos y los apoyos más comunes en construcciones tales como:

a) celosías articuladas,
b) celosías rígidas,
c) pórticos 3D.

Una celosía se denomina así a una construcción de barras plana, que está cargada perpendicularmente al plano de las vigas de la celosía. Según el tipo de conexión de las vigas, podemos distinguir:

a) celosías articuladas

Las vigas de la celosía están conectadas entre sí mediante articulaciones, de modo que pueden girar libremente una respecto a la otra. Esta conexión solo permite que el balancín que une las vigas transmita fuerza vertical (perpendicular al plano de las vigas de la celosía).
Debido a que la carga de la celosía actúa perpendicular al plano de las vigas y a que las vigas entre sí sólo transmiten fuerza transversal, en la celosía articulada sólo aparecen fuerzas transversales y momentos flectores. Esto influye en qué reacciones pueden aparecer en los apoyos. De este modo, podemos distinguir los siguientes apoyos:

- apoyo articulado

Aquí no importa si está dibujado como deslizante o no, no marcamos reacciones en el plano de la celosía, solo la reacción fuera del plano.

Fig.15. Formas de marcar un apoyo articulado en una celosía articulada

- patín vertical

A continuación, se muestra un patín vertical en dos direcciones, junto con la reacción en forma de momento, indicado de dos maneras – como vector de momento y como momento en una “notita” – ambas notaciones son equivalentes. En el patín no hay reacción vertical, en las celosías generalmente omitimos las reacciones en el eje de las vigas, así que aquí solo tenemos reacción en forma de momento – y es un momento flector para la barra, ya que las celosías articuladas no transmiten torsión (debido a las conexiones articuladas).

Fig.16. Patín vertical con reacciones para una celosía articulada

- empotramiento completo

En el empotramiento de una celosía articulada tenemos una reacción en forma de momento flector para la viga y una fuerza vertical. Abajo se muestra la reacción en forma de momento, representada en una figura de dos maneras.

Fig.17. Empotramiento completo con reacciones para una celosía articulada

Encontrarás soluciones de problemas con celosías articuladas en el Curso online mecánica de estructuras – específicamente en este apartado. Estos están sujetos a suscripción (una suscripción da acceso a todos los materiales del sitio – es decir, a todos los cursos online).

b) celosías rígidas

En las celosías rígidas, las vigas están conectadas rígidamente (podemos imaginar que las barras están hormigonadas entre sí). La flexión de las vigas dispuestas en una dirección provoca flexión y torsión de las vigas en la otra dirección.

En las celosías rígidas tenemos los mismos apoyos que en las celosías articuladas, pero aquí la diferencia es que también tenemos torsión. Por lo tanto, en el empotramiento además del momento flector habrá también una reacción en forma de momento torsor. También tendremos más opciones de patines (ya sea que bloqueen la flexión, la torsión, o ambas).

Tipos de apoyos en celosías rígidas:

- apoyo articulado

Exactamente igual que en la celosía articulada. No importa si se dibuja como deslizante o no – no marcamos reacciones en el plano de la celosía, solo la reacción fuera del plano.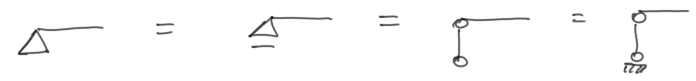

Fig.18. Formas de marcar un apoyo articulado en una celosía rígida

- patín vertical

Como se mencionó antes, tenemos tres tipos de patines en una celosía rígida:

- con reacción en forma de momento torsor,
- con reacción en forma de momento flector,
- con ambas reacciones mencionadas.

Aquí tenemos otra forma de marcar el patín distinta a la anterior, en la literatura es difícil encontrar este caso para una celosía rígida, pero la notación mostrada abajo parece razonable. También coincide con la que aparece, por ejemplo, en el programa Robot Structural Analysis.

Fig.19. Patines verticales con reacciones para celosía rígida

La primera notación se puede usar a menudo como empotramiento completo, por lo que lo mejor es aclarar, si es posible, qué tipo de apoyo tiene en mente la persona que dibujó el problema.

- empotramiento completo

Si quisiéramos aplicar de manera coherente la notación similar a la del patín, deberíamos marcar el empotramiento completo como se muestra a la izquierda, sin embargo, creo que lo más popular seguirá siendo la notación más simple que encontramos antes – la mostrada a la derecha.

Fig.20. Empotramiento completo en una celosía rígida con reacciones

c) pórticos 3D

En un pórtico espacial (3D) tenemos 6 restricciones, por lo que las reacciones pueden ser recibidas por estas restricciones en diferentes configuraciones. Lo más frecuente es encontrarnos con un empotramiento completo y con barras de apoyo corrientes que eliminan la posibilidad de movimiento en la dirección en la que están colocadas.
A continuación, algunas posibilidades de apoyos:

- barra de apoyo/apoyo articulado deslizante

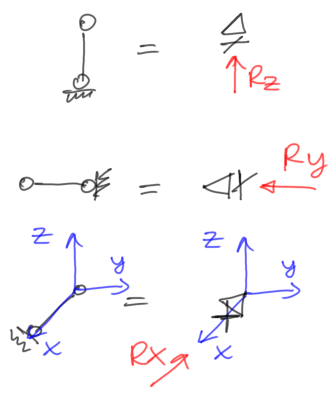
Fig.21. Bloqueo del movimiento en una dirección con su reacción

En un mismo lugar puede haber uno, dos o tres bloqueos de dirección, así que ahora la variante con dos bloqueos en un mismo punto:

- barras de apoyo/apoyo articulado deslizante

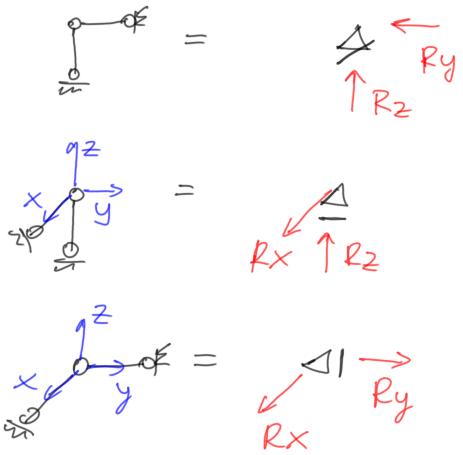
Fig.22. Bloqueo del movimiento en dos direcciones con sus reacciones

- apoyo articulado no deslizante

Fig.23. Apoyo articulado no deslizante con sus reacciones

- empotramiento completo

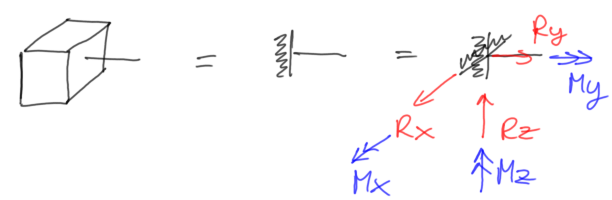
Fig.24. Empotramiento completo con sus reacciones

Con otros tipos de apoyo diferentes a los mencionados en los sistemas espaciales es poco probable que se encuentren (al menos yo no me he topado con ellos). En principio, se puede bloquear cualquier combinación de dirección lineal u orientación rotacional, por ejemplo:

Fig.25. Diferentes combinaciones de bloqueos del movimiento lineal y de rotación con sus reacciones

y así sucesivamente.