Lista zadań
Ejemplo 1
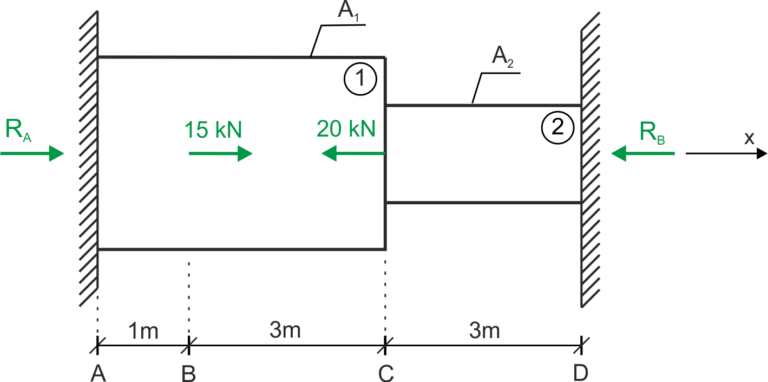
El poste de dos grados se ha asegurado permanentemente en el extremo A, el extremo D y se ha cargado con fuerzas como se muestra en la figura. Calcular la reacción en las fijaciones y señalar en qué parte del poste se generan las mayores tensiones. Datos: \( A_1=2\cdot A_2, 2\cdot E_1=E_2 \)
Ejemplo 2
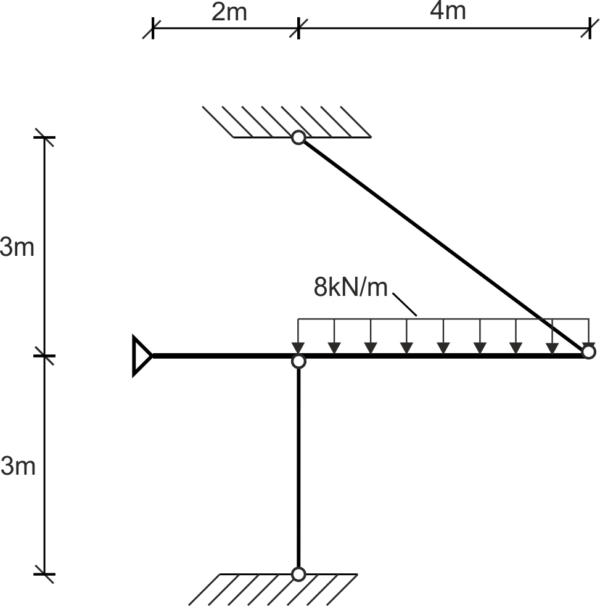
La viga fijada con articulaciones y sujeta por dos barras está cargada con una carga continua. A partir de la condición de resistencia, calcule el diámetro de las barras. Datos: \( A_1=A_2, E_1=2\cdot E_2, k_r=60\ MPa, k_c=90\ MPa \)
Ejemplo 3
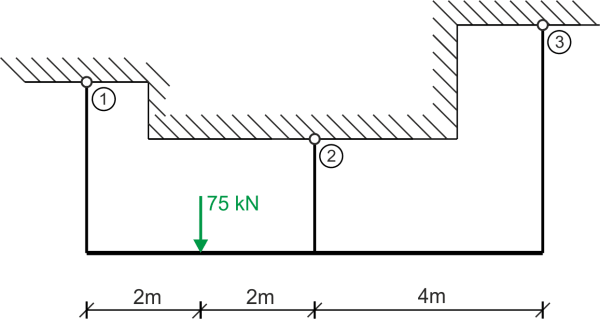
La viga de madera está suspendida en tres barras: la primera y la tercera están hechas de acero, mientras que la segunda es de cobre, con longitudes \( l_1=3m, l_2=2m, l_3=4m \). Calcula las tensiones que se generan en las barras. Datos: \( k_{r_s}t=120 MPa, k_{r_m}=30 MPa, A_1=A_2=2\cdot A_3, E_2=105 GPa, E_1=E_3=210 GPa\)
Ejemplo 4
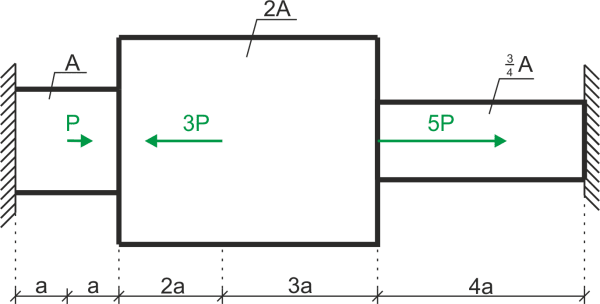
Calcula las fuerzas normales y dimensiona el área de la sección transversal de la barra. Datos: P, k.
Ejemplo 5
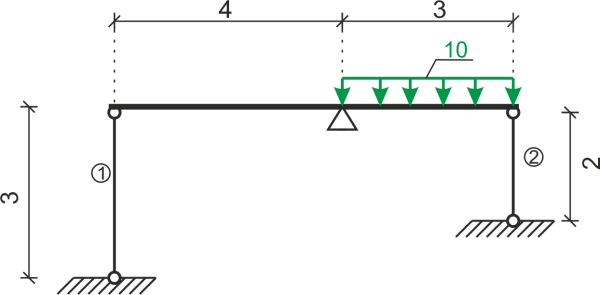
Calcula el diámetro de los cables en los que se apoya la viga. Datos: \( E=210 GPa, A_1=A_2, k_r=100 MPa, k_c=120 MPa \)
Ejemplo 6
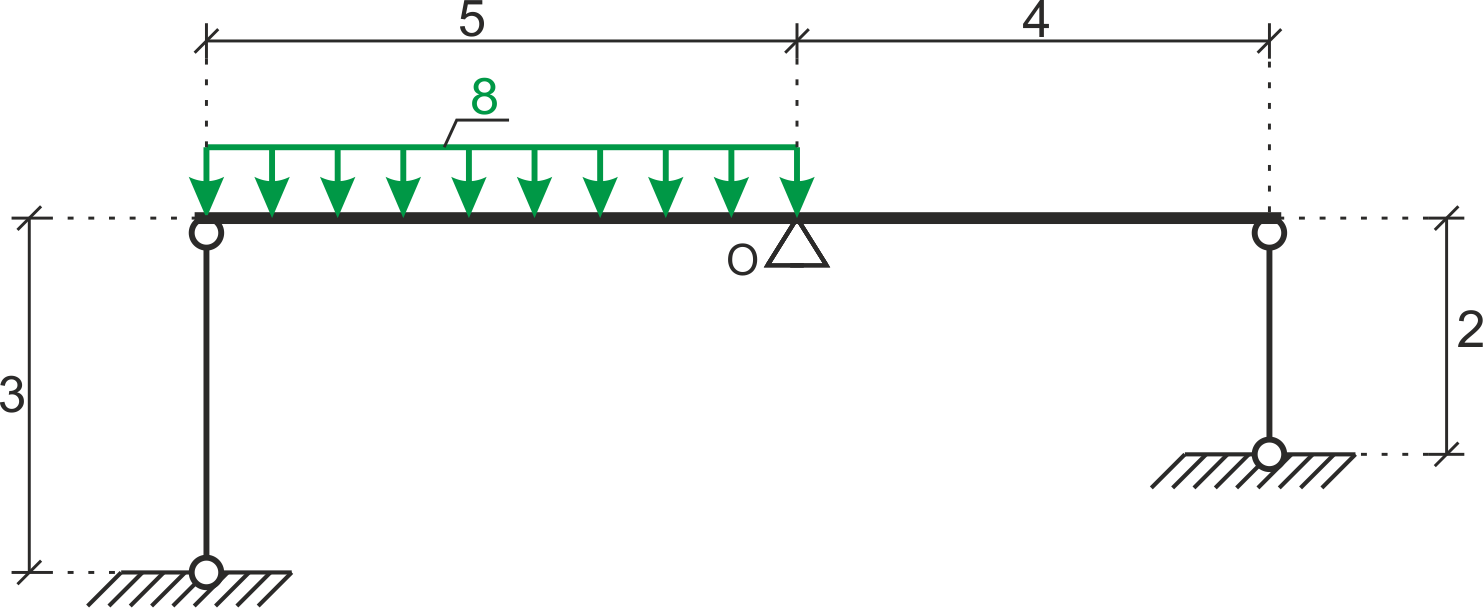
Calcule las fuerzas en las barras que sostienen la viga. Datos: \( A_1=A_2=A, E_1=E_2=E \)
Ejemplo 7
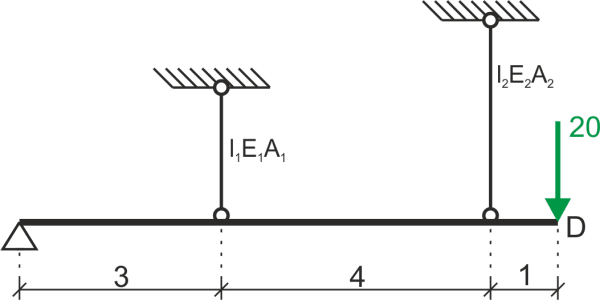
Calcula el desplazamiento vertical del punto D.\n Datos: \( E_1=2\cdot E_2, E_1=210\ GPa, l_1=2 m, l_2=3 m, 2\cdot A_1=A_2, A_1=20 cm^2 \)
Ejemplo 8
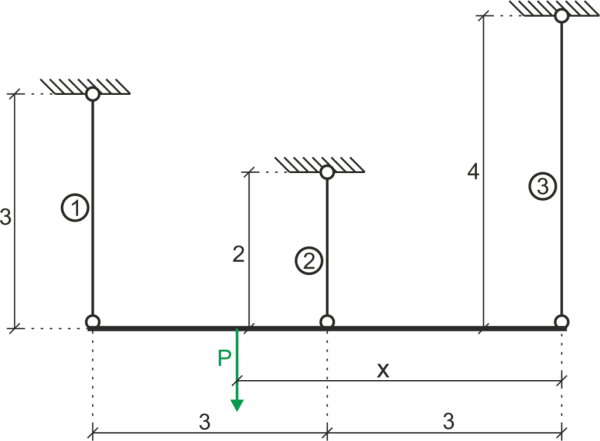
En qué distancia \(x\) desde la barra número 3 se debe aplicar la fuerza \(P\) para que la viga se mueva hacia abajo paralelamente. Datos: \(E_1=E_3=210 GPa, E_2=110 GPa, A_1=A_2=2\cdot A_3, P=20 kN\)
Ejemplo 9
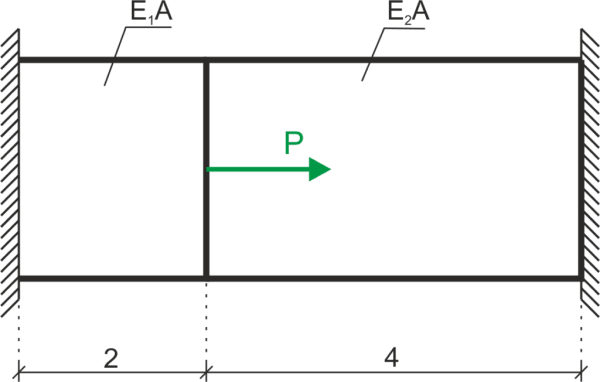
Calcular las fuerzas normales en la barra siguiente. Datos: \(P=20 kN, E_1=2,1\cdot 10^5 MPa, E_2=1\cdot 10^5 MPa\)
Ejemplo 10
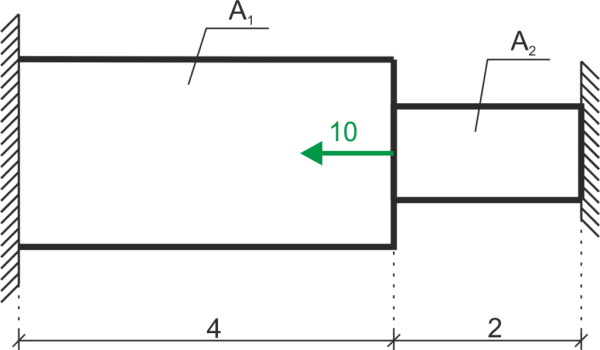
Calcula la reacción en el soporte del lado izquierdo debido a la carga estática y térmica, y dibuja el diagrama de fuerzas normales. Calcula las tensiones en dos intervalos de la barra. Datos: \(\Delta_T=20^o\ C, \alpha=1,2\cdot 10^{-5}, E=205\cdot 10^9, A_1=20\ cm^2, A_2=15\ cm^2\)
Ejemplo 11
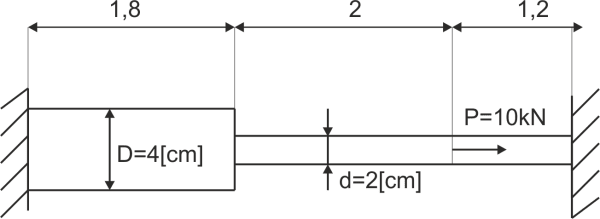
Calcula y dibuja el diagrama de las fuerzas normales, tensiones y elongaciones en todos los intervalos del eje de dos etapas. Los datos se proporcionan en la figura. Todo el eje se calentó \(20^o C\). El coeficiente de expansión térmica es \(\alpha = 1,2\cdot 10^{-5}\)
Ejemplo 13
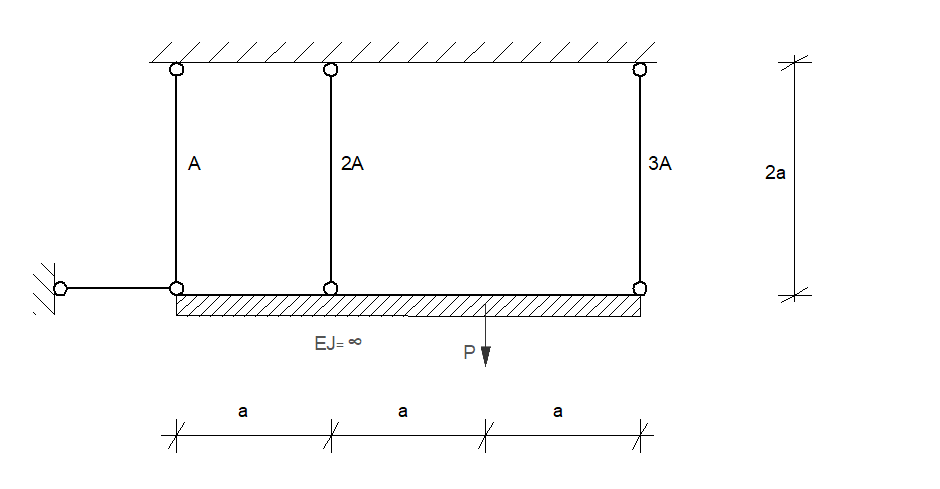
Determinar la capacidad de carga elástica \( P = P_s \) y la límite \( P = P_n \). Determinar la capacidad de carga límite utilizando el enfoque estático y cinemático. Verificar si la solución obtenida es completa. Además, determinar el coeficiente de reserva de capacidad de carga \( m = \frac{P_n}{P_s} \). Al presentar los resultados finales, considerar: \( a = 1 \, \text{m} \), \( A = 4 \, \text{cm}^2 \), \( R_{pl} = 200 \, \text{MPa} \).