Aplicar el MES para resolver (calcular los grados de libertad) el problema de Laplace (\(f = 0\)) en el área discretizada con dos elementos finitos iguales \([1], [2]\) y nodos numerados como en la figura, \(h = 3\).

Aceptar en parte del borde (1-2-3) condiciones de tipo Dirichlet \( \hat{T} = 3y \) y en el resto condiciones de tipo Neumann \( \hat{q} = 0 \).

El elemento \([1]\), con nodos 1, 2, 4, tiene la matriz de rigidez \( K^{el1} = [[MATH_0_BLK]] \).

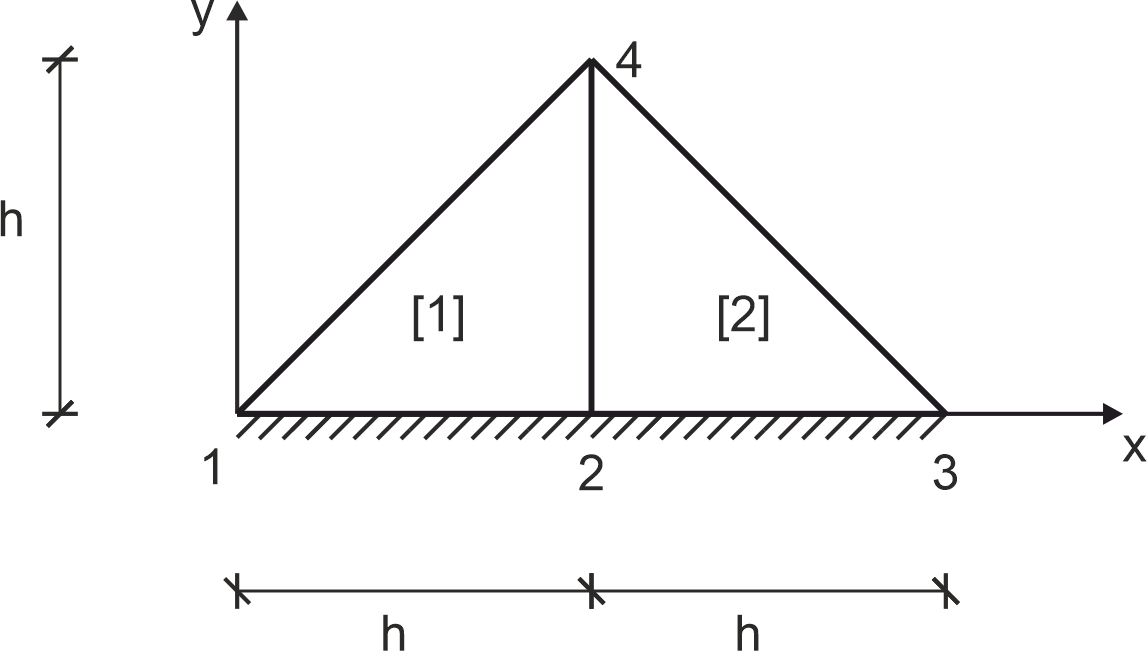
Aplicar el MES para resolver (calcular los grados de libertad) el problema de Laplace (\(f = 0\)) en el área discretizada con dos elementos finitos iguales \([1], [2]\) y nodos numerados como en la figura, \(h = 2\).

Aceptar en parte del borde (1-2-3) condiciones de tipo Dirichlet \( \hat{T} = 2x \) y en el resto condiciones de tipo Neumann \( \hat{q} = 0 \).

El elemento \([1]\), con nodos 1, 2, 4, tiene la matriz de rigidez \( K^{el1} = [[MATH_0_BLK]] \).