Lista zadań
Ejemplo 2
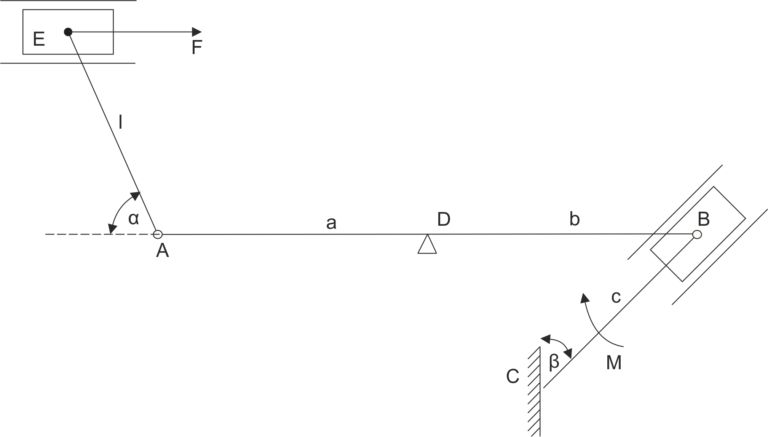
Se proporciona un sistema de tres barras articuladas. La barra inferior está libremente soportada en un soporte. Libera el sistema de restricciones y escribe las ecuaciones de equilibrio estático.
Ejemplo 3
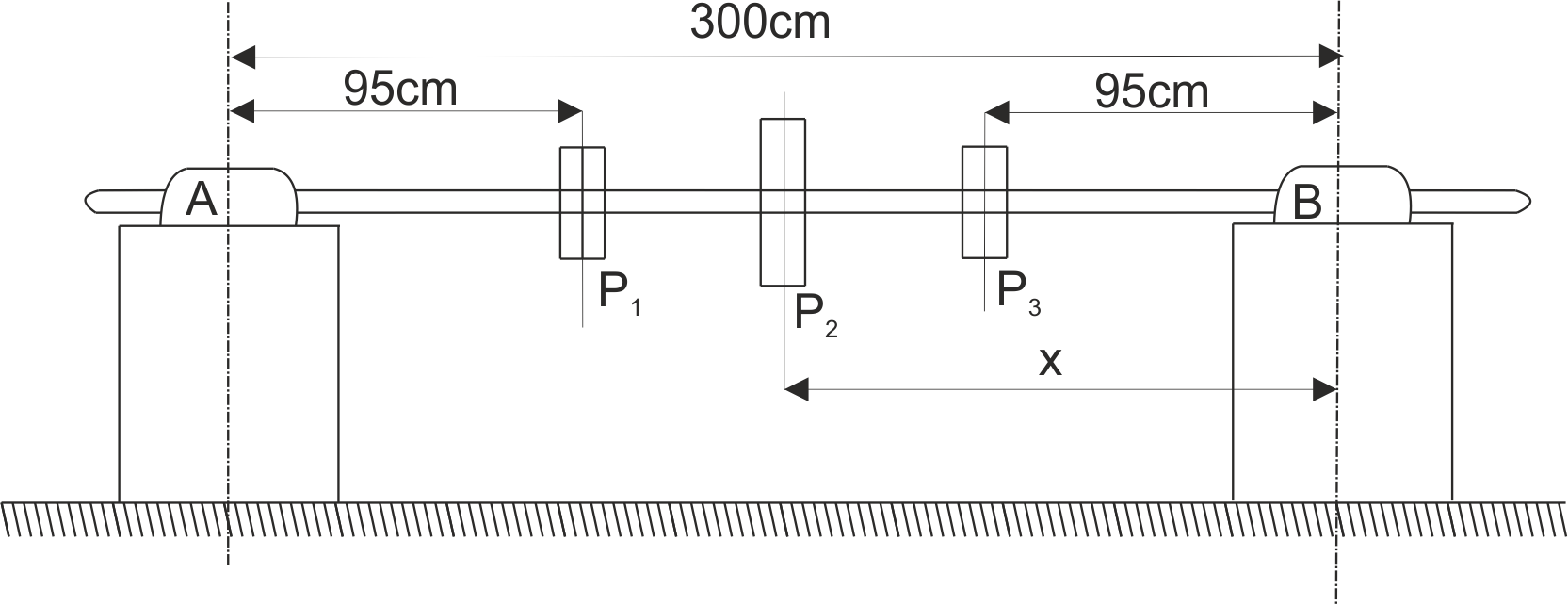
El eje de transmisión AB tiene tres poleas con pesos P1=3 kN, P2=5 kN, P3=2 kN. Las dimensiones se muestran en la figura. ¿A qué distancia x del cojinete B se debe colocar la polea con peso P2 para que las reacciones de ambos cojinetes sean iguales? Se pasa por alto el peso del eje.
Ejemplo 4
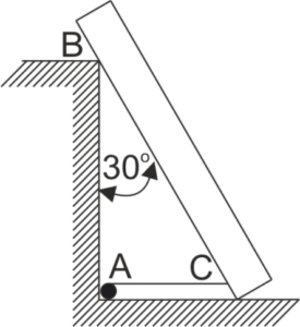
Una viga homogénea con una masa de 60 kg y una longitud de 4 m, apoyada en un extremo en el suelo liso y en un punto intermedio B en un poste de 3 m de altura, forma un ángulo de \(30^o\) con la vertical. La viga se mantiene en esta posición mediante una cuerda AC que atraviesa a lo largo del suelo. Determinar la fuerza T en la cuerda y las reacciones en los puntos B y C.
Ejemplo 5
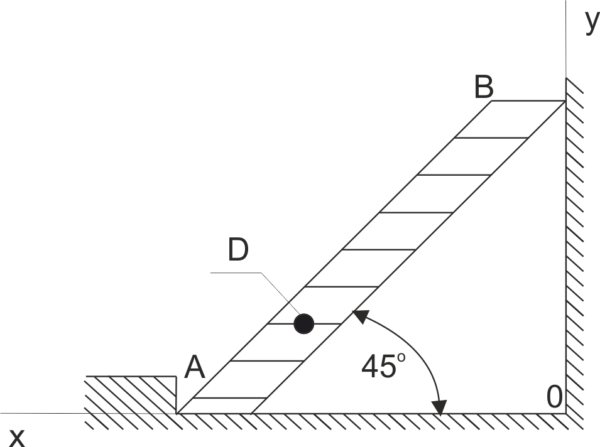
Para una pared lisa se coloca una escalera AB, inclinada a un ángulo de 45^o con respecto al nivel del suelo. La escalera tiene una masa de 20 kg. En el punto D, que está a 1/3 de la longitud de la escalera desde el extremo inferior, hay una persona con una masa de 60 kg. Calcular las fuerzas de presión de la escalera sobre el soporte A y sobre la pared.
Ejemplo 6
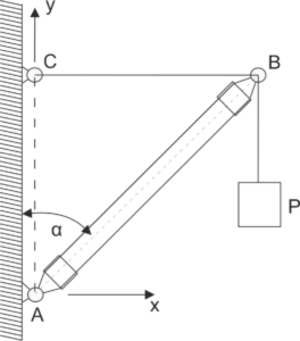
El elevador está compuesto por una viga AB, cuyo extremo inferior está conectado por una articulación A a la pared, y el extremo superior es sostenido por una cuerda horizontal BC. Determinar la tensión T de la cuerda BC y la proyección vertical \(N_A\) de la fuerza de apoyo en el soporte A, si la carga P es igual a P=2 kN, el peso de la viga Q=1 kN está enganchado en el punto medio de la longitud AB, y el ángulo \( \alpha=45^o \).
Ejemplo 7
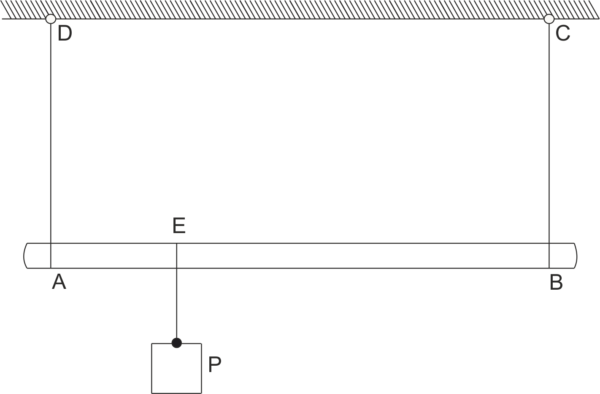
Una barra AB homogénea de 1 m de longitud y peso 20 N está suspendida horizontalmente en dos cuerdas paralelas AC y BD. En el punto E de la barra, que está a una distancia de 0,25 m del punto A, se cuelga un peso P = 120 N. Calcula las fuerzas en las cuerdas \( T_{AC}, T_{BD} \).
Ejemplo 8
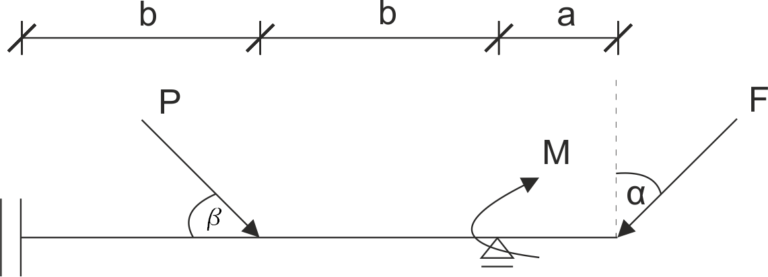
Se da una viga soportada por un patín vertical y un soporte articulado deslizante. Libera el sistema de restricciones y escribe las ecuaciones de equilibrio estático.
Ejemplo 9
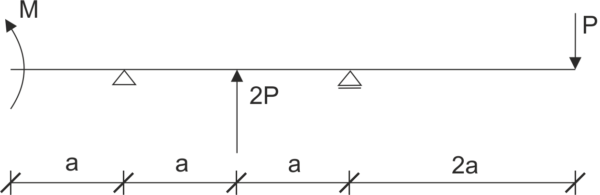
Dada una viga apoyada como en la imagen. Libera el sistema de restricciones y escribe las ecuaciones de equilibrio.
Ejemplo 10
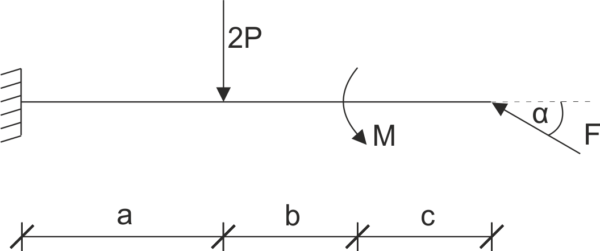
Dada una viga soportada como se muestra en el dibujo. Libera el sistema de restricciones y escribe las ecuaciones de equilibrio.
Ejemplo 11
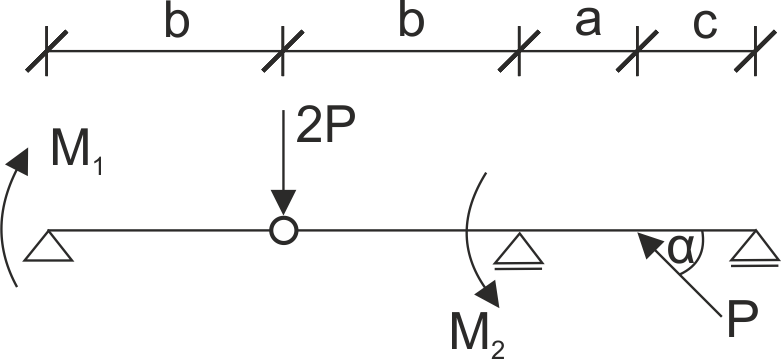
Se da una viga apoyada como se muestra en la imagen. Libere el sistema de restricciones, divida la viga articulada en vigas simples y escriba las ecuaciones de equilibrio.
Ejemplo 12
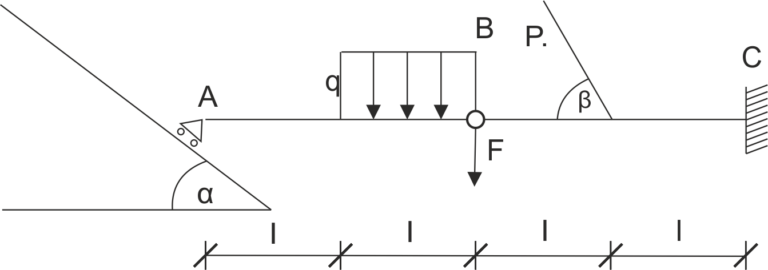
Se proporciona una viga soportada como se muestra en la figura. Libera el sistema de las restricciones, divide la viga articulada en vigas rectas y escribe las ecuaciones de equilibrio.