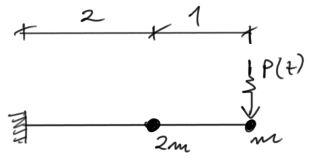
Para la viga dada, determinar las frecuencias naturales de vibración y dibujar sus modos de deformación. Verificar la condición de ortogonalidad. Dibujar los momentos finales causados por las fuerzas de inercia (tomar la frecuencia de excitación como el promedio aritmético de las frecuencias naturales calculadas anteriormente, es decir, \( \theta=\frac{\omega_1+\omega_2}{2} \) ) \( \text{Datos:} \ EI= 2,1\cdot 10^5 \ kNm^2, \ m=200 \ kg, \ P=10\cdot sin(\theta \ t) \)

Para el marco dado, calcular las fuerzas de inercia. \( \text{Datos:} \ EI= 4000 \ kNm^2, \ m=700 \ kg, \ P=25 sin(pt), \ p=15\ \frac{rad}{s} \)

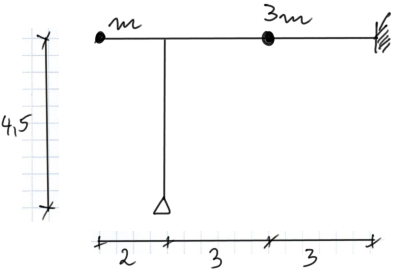
Para el marco dado, dibujar los momentos finales provenientes de las fuerzas de inercia. Dibujar las envolventes de momentos. Datos: \( \mathrm{E}=2.1 \cdot 10^{11} \frac{\mathrm{N}}{\mathrm{m}^2}, \mathrm{~m}=660 \mathrm{~kg}, \mathrm{~m}_{\mathrm{w}}=2250 \mathrm{~kg}, \mathrm{e}=4.3 \mathrm{~mm}, \mathrm{n}=470 \frac{\mathrm{obr}}{\mathrm{min}} \), sección de viga IPN 200.

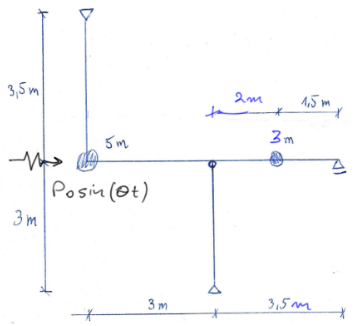
Para el marco dado, dibuje los momentos finales causados por las fuerzas de inercia. Dibuje las curvas de los momentos. Datos: \( \mathrm{E}=2.1 \cdot 10^{11} \frac{\mathrm{N}}{\mathrm{m}^2}, \mathrm{~m}=680 \mathrm{~kg}, \mathrm{~m}_{\mathrm{w}}=400 \mathrm{~kg}, \mathrm{e}=2 \mathrm{~mm}, \mathrm{n}=300 \frac{\mathrm{obr}}{\mathrm{min}} \), sección transversal del marco con momento de inercia \(I=4250\ cm^4 \).

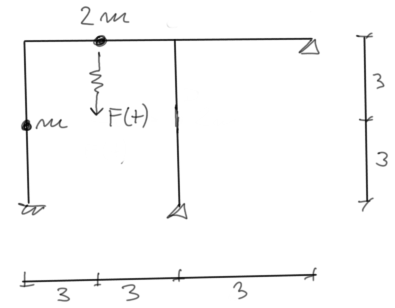
Para el marco dado, dibujar los momentos finales provenientes de las fuerzas de inercia. Datos: \( \theta =0,8\cdot \omega_1 \, F_0=2\ kN \)

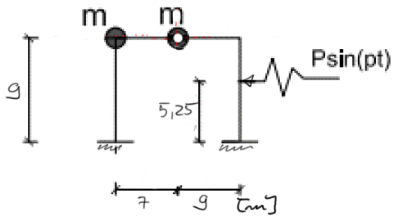
Para el marco dado, dibuje los momentos finales provenientes de los ejes de inercia. Verifique si las tensiones en la barra de sección rectangular de 12 x 24 cm y módulo de Young de 210 GPa no superan la resistencia permitida de 240 MPa. Datos: \( \mathrm{p}=8.25 \frac{\mathrm{rad}}{\mathrm{s}}, \mathrm{m}=2.75 \mathrm{t}, \mathrm{P}=20.5 \mathrm{kN} \)