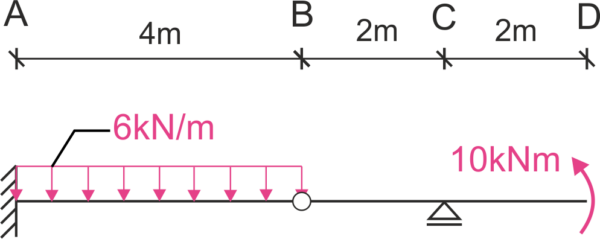
Calcula el desplazamiento vertical del punto D (\(\Delta_D\)). Ten en cuenta el efecto de los momentos de flexión y de las fuerzas cortantes.

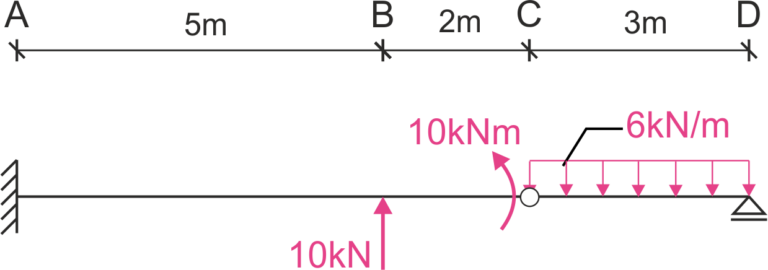
Calcula el ángulo de rotación del punto D \(\varphi_D.\) Ten en cuenta el efecto de los momentos de flexión y las fuerzas cortantes.

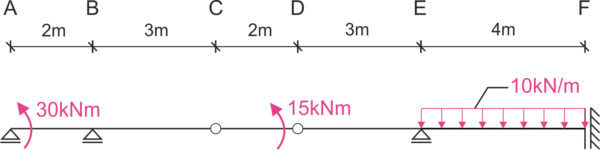
Calcular la desplazamiento vertical del punto C \( \Delta_C \), el desplazamiento vertical del punto D \( \Delta_D \), el cambio en el ángulo de rotación del punto C \( \Delta\varphi_C \). E=210GPa, I=6500cm^4. Tenga en cuenta solo la influencia de los momentos de flexión.

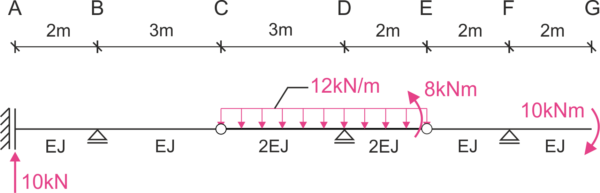
Calculate the vertical displacement of point C \( \Delta_C \), the angle of rotation at point G \(\varphi_G \), and the change in angle of rotation at point C \( \Delta\varphi_C. E=210 GPa, I=7500cm^4 \) Consider only the influence of bending moments.

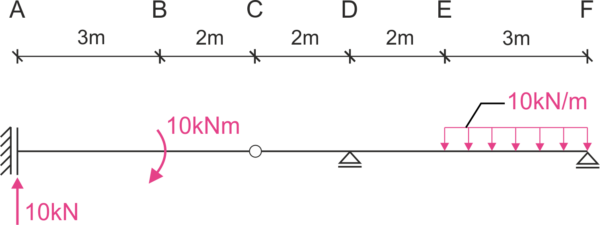
Calcular el desplazamiento vertical del punto A \( \Delta_A\) , el desplazamiento vertical del punto E \( \Delta_E\) , el ángulo de giro en el punto F \( \varphi_F \) y el cambio en el ángulo de giro en el punto C \( \Delta\varphi_C.\) Tener en cuenta el efecto de los momentos flexionantes. \( E=200 GPa , I=5000cm^4 \)

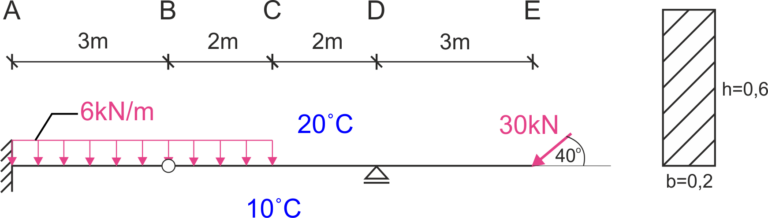
Calcular el desplazamiento vertical del punto C (\( \Delta_C \)), el desplazamiento horizontal del punto E (\( \Delta_E \)) y el cambio en el ángulo de rotación en el punto B (\( \Delta\varphi_B \)). Tener en cuenta la influencia de los momentos de flexión, las fuerzas normales y la temperatura. Datos: \( b=0,2m, h=0,6m, E=205 GPa, \nu=0,3, t_g=20^oC, t_d=10^oC, \alpha=1,2\cdot 10^{-5}, \kappa=1,2 \)

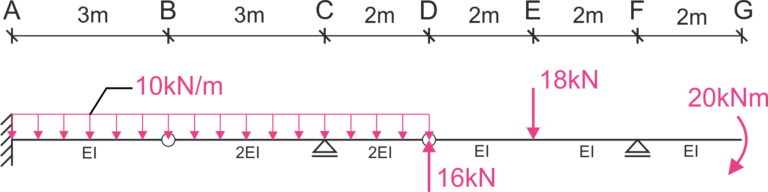
Calcular el ángulo de rotación del nodo C \(\varphi_C\), el desplazamiento vertical del punto G \(\Delta_G\), el desplazamiento vertical del punto D \(\Delta_D\) y el cambio de ángulo de rotación en el punto D \(\Delta\varphi_D.\) Tenga en cuenta la influencia de los momentos de flexión y preste atención a las características diferentes de las secciones. \(E=210GPa, I=7650 cm^4\)