Internal Forces in Frames



From this course, you will learn:
- how to determine support reactions in frames,
- how to check the correctness of the calculated reactions,
- how to draw diagrams of normal forces, shear forces, and bending moments in straight, inclined, and hinged frames,
- how to check the equilibrium of a node (checking the correctness of the diagrams),
- how to draw diagrams using two methods – one involving writing down internal force functions and one without writing them,

all of this starting from very simple frame examples, moving on to frames with more and varied loads, and finishing with frames with inclined members both with and without hinges.

Internal forces in frames

In the field of strength of materials, understanding internal forces is a key element for structural design and analysis. Internal forces such as axial force, shear force, and bending moment are fundamental values that shape how materials behave under load.

Similar to beams, frames are also subjected to these same internal forces, influencing their strength and stability. Analyzing these forces helps engineers better understand how frames behave under various loading conditions and design them accordingly.


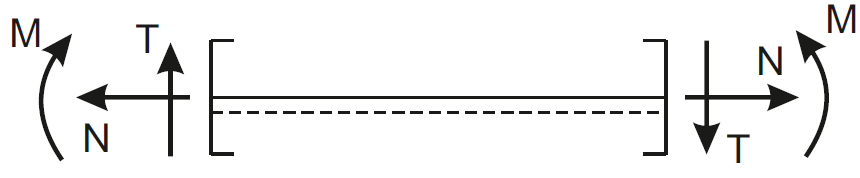
Fig. 1. Sign convention for internal forces


Frames are extremely versatile and are used in many different types of structures, from residential and commercial buildings to bridges, sports halls, and infrastructure components. Their use allows for the creation of durable, stable, and aesthetically pleasing structures that can withstand a variety of loads and environmental conditions.

Computational challenges

From the standpoint of internal force calculations, computing frames is a bit more difficult than computing beams.

First, once we learn how to use the sign convention going from the left or right side of a beam, we encounter an initial issue interpreting the convention for a vertical member.
Perhaps the simplest approach at first is to draw what's often called the "underside" of the member on the sign convention diagram, meaning an arbitrary “bottom” of the member. If, when solving a frame, we also mark an underside on the vertical member (on any side), it will be easier to apply the sign convention. We can always rotate the page so that we look at the vertical member as if it were a horizontal beam — assuming we already know how to compute beams.

Another issue arises if we have an inclined member, because up until now for a horizontal member (a beam), if a force acted along the beam axis (horizontally), it was the axial force, and if it acted perpendicular to the beam (vertically), it was the shear force.
For a vertical member, on the other hand, vertical forces were axial forces, and horizontal ones were shear relative to the member.
For an inclined member – if we load it with a horizontal force, we must resolve that force into a component along the member’s axis (the normal component to the member) and perpendicular to the axis (the shear component). This introduces another skill we need to master to properly draw the diagrams: resolving forces into components.

A good check for correctness of the drawn internal force diagrams is to verify the equilibrium of a node, which we will show in the example below.

A video course showing how to draw internal force diagrams
for a hinged frame with an inclined member, writing down internal force functions.

Below is a solution with a description of resolving forces into components for the inclined member and verifying the node equilibrium at the end

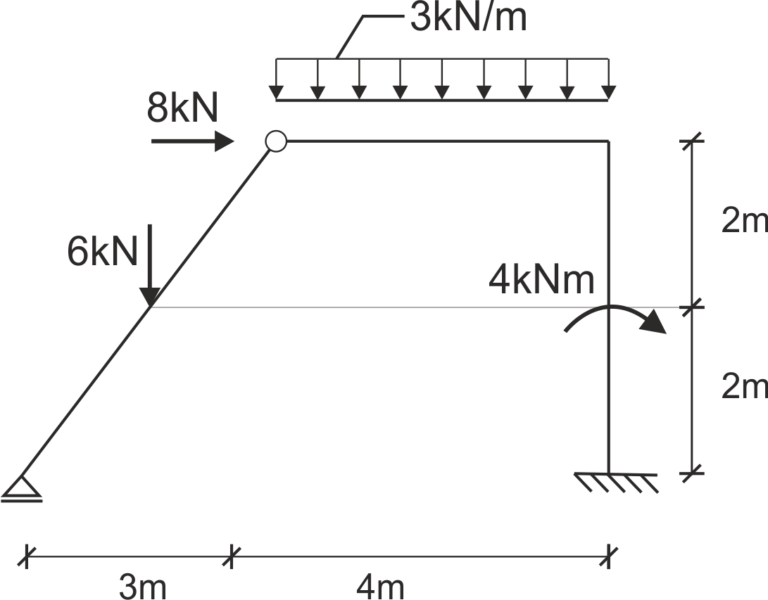
Inclined frame topic

Solution

1) Marking the undersides, labeling characteristic points, marking the support reactions and calculating them
As mentioned in the introduction – we mark the undersides of the frame.
For clarity, we label the characteristic points and make sure to mark the reactions – we will be calculating them next.

Static equilibrium equations

\begin{aligned} &\sum M_{C}^L = 0\\ &-6 \cdot \frac{3}{2} + V_{A} \cdot 3 = 0\\ &V_{A} = \frac{6 \cdot \frac{3}{2}}{3} = 3 \, \text{kN}\\ \end{aligned} \( \quad \quad \) \begin{aligned} &\Sigma X = 0\\ &8 + H_{F} = 0\\ &H_{F} = -8 \, \text{kN}\\ \end{aligned}
\begin{aligned} &\Sigma Y = 0\\ &V_{A} - 6 - 3 \cdot 4 + V_{F} = 0\\ &V_{F} = -\left(V_{A} - 6 - 3 \cdot 4\right) = 15 \, \text{kN}\\ \\ &\Sigma M_{A} = 0\\ &6 \cdot \frac{3}{2} + 8 \cdot 4 + 3 \cdot 4 \cdot 5 + 4 - V_{F} \cdot 7 + M_{F} = 0\\ &M_{F} = -\left(6 \cdot \frac{3}{2} + 8 \cdot 4 + 3 \cdot 4 \cdot 5 + 4 - V_{F} \cdot 7\right) = 0 \, \text{kNm} \end{aligned}
2) Calculating the internal forces
With the reactions calculated, we move on to calculating the internal forces. Here we will show how to resolve the force on the inclined member into normal and shear components relative to the member.

Resolving VA into the normal and shear directions of the member
A good idea is to make a diagram that shows the vertical direction, horizontal direction, the axis of the member (normal direction), and perpendicular to the axis of the member (shear direction).
We define angle alpha by looking at the frame between the horizontal and the member’s axis.
Additionally, we can mark the positive directions for the normal and shear forces that apply when analyzing the inclined member from point A.

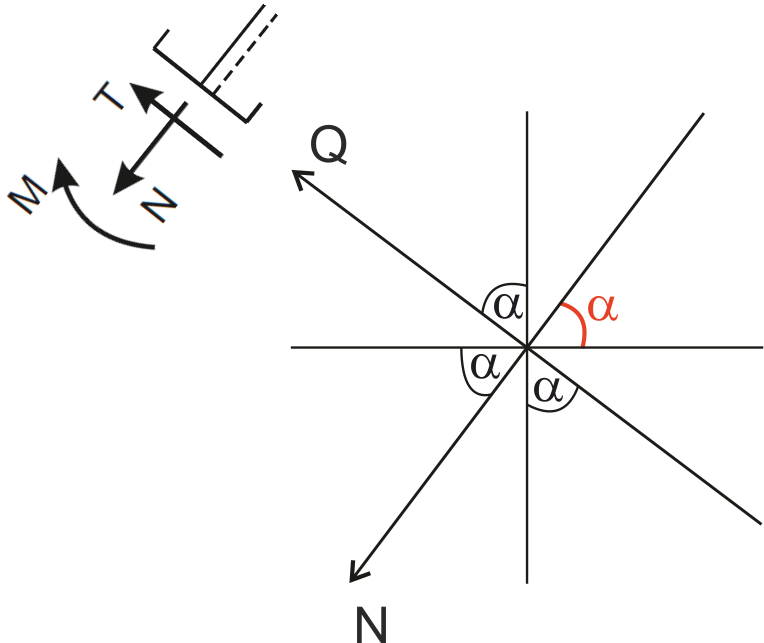
In such a diagram, every other angle is alpha.

Now, if we want to resolve the reaction \( V_A=3 \ kN \) into the normal and shear directions of the member, we place it on this “web” at the top.
The two nearest components are the normal and shear ones. Most importantly, remember that the component adjacent to the angle alpha is multiplied by the cosine of that angle, and the other component is multiplied by the sine of alpha.
See the figure below.


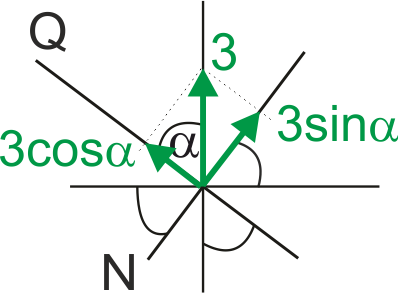
So, we basically have all we need. We write down the internal force functions in all the segments:

Segment AB \( 0 \leq x \leq 1.5\)

 \( \quad \quad \)
\begin{aligned} &Q(x) = 3 \cos (\alpha) = 1.8 \, \text{kN} \\ &M(x) = 3x \\ &M(0) = 0 \\ &M(1.5) = 4.5 \, \text{kNm} \\ &N(x) = 3 \sin (\alpha) = -2.4 \, \text{kN} \end{aligned}

Segment BC \( 1.5 \leq x \leq 3\)

 \( \quad \quad \)
\begin{aligned} &Q(x) = 3 \cos (\alpha) - 6 \cos (\alpha) = -1.8 \, \text{kN} \\ &M(x) = 3x - 6 \cdot(x - 1.5) \\ &M(1.5) = 4.5 \, \text{kNm} \\ &M(3) = 0 \\ &N(x) = 3 \sin (\alpha) + 6 \sin (\alpha) = -2.4 \, \text{kN} \end{aligned}

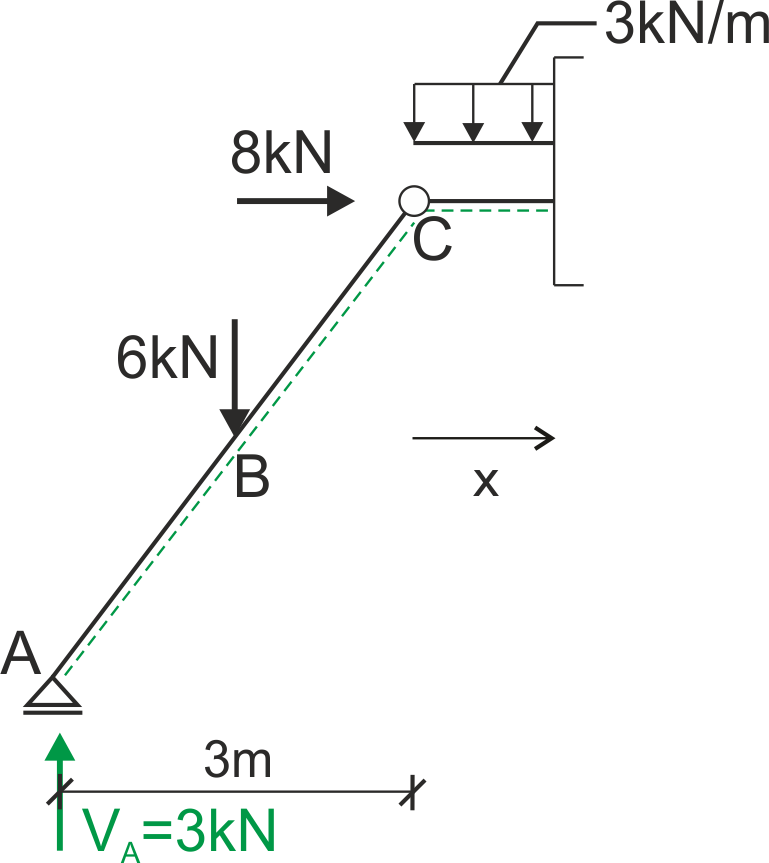
Segment CD \( 0 \leq x \leq 4\)

 \( \quad \quad \)
\begin{aligned} & \mathrm{N}(\mathrm{x})=-8 \ \mathrm{kN} \\ & \mathrm{Q}(\mathrm{x})=3-6-3 \cdot \mathrm{x}=-3 \cdot \mathrm{x}-3 \\ & \mathrm{Q}(0)=-3 \ \mathrm{kN} \\ & \mathrm{Q}(4)=-15 \ \mathrm{kN} \\ & \mathrm{M}(\mathrm{x})=3 \cdot(3+\mathrm{x})-6 \cdot(1.5+\mathrm{x})-3 \cdot \mathrm{x} \cdot \frac{\mathrm{x}}{2} \\ & \mathrm{M}(0)=0 \ \mathrm{kNm} \\ & \mathrm{M}(4)=-36 \ \mathrm{kNm} \end{aligned}

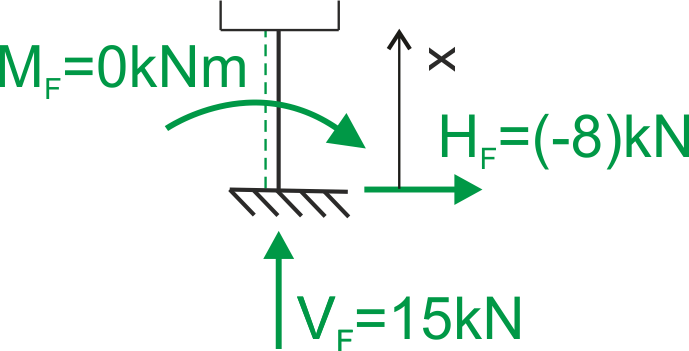
Segment FE \( 0 \leq x \leq 2\)

 \( \quad \quad \)
\begin{aligned} & \mathrm{N}(\mathrm{x})=-15 \ \mathrm{kN} \\ & \mathrm{Q}(\mathrm{x})=8 \ \mathrm{kN} \\ & \mathrm{M}(\mathrm{x})=-8 \cdot \mathrm{x} \\ & \mathrm{M}(0)=0 \\ & \mathrm{M}(2)=-16 \ \mathrm{kNm} \end{aligned}

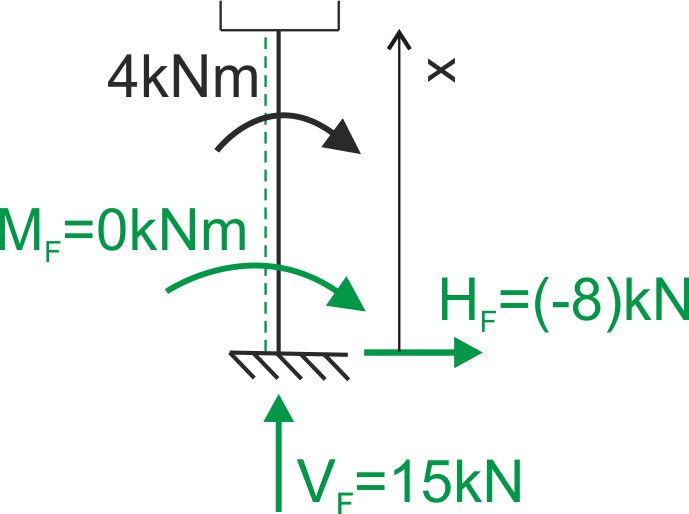
Segment ED \( 2 \leq x \leq 4\)

 \( \quad \quad \)
\begin{aligned} & \mathrm{N}(\mathrm{x})=-15 \ \mathrm{kN} \\ & \mathrm{Q}(\mathrm{x})=8 \ \mathrm{kN} \\ & \mathrm{M}(\mathrm{x})=-8 \cdot \mathrm{x}-4 \\ & \mathrm{M}(2)=-20 \ \mathrm{kNm} \\ & \mathrm{M}(4)=-36 \ \mathrm{kNm} \end{aligned}

Based on the calculated internal force values, we draw the diagrams.
3) Internal force diagrams




4) Checking node equilibrium
How to check the equilibrium of a node is shown in a separate theoretical introduction – SEE HERE.
Below, you will also find links to numerous solution examples for both simple frames and those with inclined member(s), as well as frames with hinges.