Strength of Materials - Clebsch Method



The differential equation of the deformed beam from which we start in Clebsch Method has the following form:
\(E J \frac{d^2 y}{d x^2}=-M_g\)
The product \(E J\) is a general designation of stiffness for bending, where:

- E - Young's modulus,
- J - Moment of inertia of the beam's cross-section with respect to the horizontal axis.


The sign “-” on the right side of the equation results from the adopted coordinate system
and the convention defining the sign of the bending Moment.
Specifically - the assumption of positive deflections downwards, and thus the positive direction of the deflection axis downwards.

In order to determine the deflections of the beam, we integrate the above equation twice
and obtain the first derivative - the function of the angle of rotation of the beam
\begin{gathered} \varphi=\frac{d y}{d x}=-\frac{1}{E J}\left(\int M_g d x+C\right) \\ \end{gathered}

and the second derivative - the deflection function
\begin{gathered} y=-\frac{1}{E J}\left(\int\left(\int M_g d x\right) d x+C x+D\right) \end{gathered}
where:
C and D denote the constants of integration.

The constants of integration are determined from the kinematic boundary conditions, i.e., conditions for zero deflections and angles of deflection at a specified type of support. See what types of supports there are for a beam in the plane

As we have noted, the Clebsch method, while maintaining certain conditions of notation, allows for a simple beam to obtain the equation of the deflection line containing only two unknowns (constants of integration) regardless of the number of segments.

The principles governing the application of the Clebsch method can be summarized in 4 points:

- the cuts in all segments must be measured from the same point
we adopt one coordinate system for the simple beam, we cannot write, for example, part of the function from one side and part from the other side of the beam

- in the case of a continuous load, it cannot be interrupted
if such a case occurs, the continuous load should be extended to the end of the beam, simultaneously adding the same load with the opposite sign (counter-load)
- all newly added terms in the expression for the bending Moment must contain the factor \( (x- l_{i-1}) \),
where:
\(l_{i-1}\) denotes the coordinate of the beginning of the i-th segment of the beam

- in the case of a concentrated Moment M – we multiply the Moment by the arm of action to the power of 0

\(M\cdot (x-l_{i-1})^0\),

- integration should be performed without expanding expressions in parentheses
the constants of integration apply to the entire beam (for all segments)
If the coordinates \(l_{\mathrm{i}}\) define the position of concentrated forces \(P_{\mathrm{i}}\) or the beginnings of continuous loads \(q_{\mathrm{i}}\), then expressions of the type \(P_i\left(x-l_i\right)\) or \(q_i \frac{\left(x-l_i\right)^2}{2}\) are integrated according to the scheme

\(\int\left(x-l_i\right)^n d x=\frac{\left(x-l_i\right)^{n+1}}{n+1}+C\)


In this course, you will learn
Clebsch Method (analytical):
- how to determine the Moment function for a beam for the Clebsch method,
- how to write the differential equation of the deformed axis and how to integrate it,
- how to calculate the constants of integration of the equation from boundary conditions for different types of beams,
- how to calculate deflection and angle of rotation at any point of the beam.

Statically indeterminate systems:
- how to determine reactions in a statically indeterminate beam using the Clebsch method.

And now let’s look at the example below and see the solution in practice.

See the example

Three-segment beam with different types of loads.
Calculate the deflection and angle of rotation at a given point of the beam.

Solution of the example from the video course

Content

Calculate the deflection at point A.
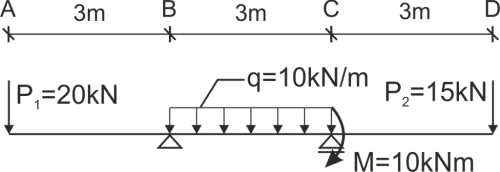
Example 1-Clebsch Method

Solution

We calculate the support reactions

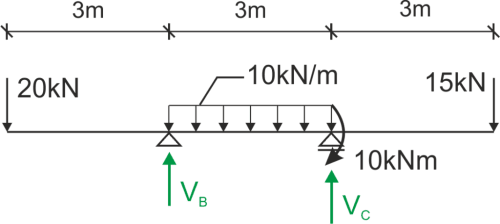\begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}

We write the Moment function from the left side.

The function can also be written from the right side. We encourage you to check this variant, calculate the sought displacement, and compare the results.

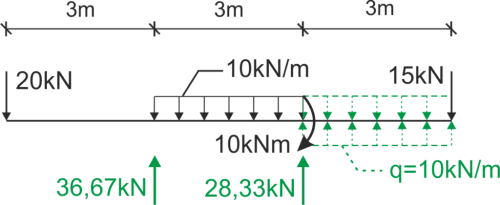\begin{aligned} &M_g(x)=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJ\cdot w"=-M_g(x)=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJ\cdot w'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJ\cdot w=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\ \end{aligned}

Boundary conditions

\begin{aligned} &w(x=3)=0 \Rightarrow 90+3C+D=0\\ &w(x=6)=0 \Rightarrow 588.735+6C+D=0\\ &C=-166,245\\ &D=408.735\\ \end{aligned}

We calculate the deflection at point A.

If we adopted the coordinate system at the left end of the beam, then point A has the coordinate x=0.

Therefore \begin{aligned} &w_A(x=0)=\frac{1}{EI}\cdot (D)\\ \end{aligned} \begin{aligned} &w_A=\frac{1}{EI}\cdot (408.735)\\ \end{aligned}