Edupanda » Numerical Methods » Finite Difference Method (FDM)
Finite Difference Method (FDM)
A method that involves approximating the derivative of a function using appropriate difference formulas. In the following study, we will focus on two simple applications of the finite difference method:
- Solving differential equations
- Solving bending beams
We convert individual derivatives into difference formulas using the following formulas:
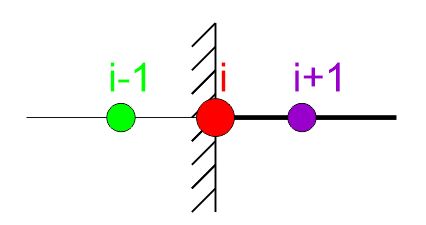
Central Difference Formulas for the One-Dimensional Problem

\begin{aligned} &f^I=\frac{1}{2 h}\left(-v_{i-1}+v_{i+1}\right) \\ &f^{I I}=\frac{1}{h^2}\left(v_{i-1}-2 v_i+v_{i+1}\right) \\ &f^{I I I}=\frac{1}{2 h^3}\left(-v_{i-2}+2 v_{i-1}-2 v_{i+1}+v_{i+2}\right) \\ &f^{I V}=\frac{1}{h^4}\left(v_{i-2}-4 v_{i-1}+6 v_i-4 v_{i+1}+v_{i+2}\right) \end{aligned}
where \( h \) - length of the element.
Solving Differential Equations with the Finite Difference Method
The general procedure in this case is as follows:
- Divide the interval of interest into n elements of length h
- Replace derivatives in the equation with appropriate difference formulas
- Write down difference equations for each point
- Consider boundary conditions
- Solve the system of equations in matrix form

Example 1
Content
Solve the boundary problem with the following data
\begin{aligned} &y^{\prime \prime}(x)=2 x \quad x \in[a . b] \\ &a=3 \quad b=7 \\ &y(a)=4 \\ &y^{\prime}(b)=2 \\ \end{aligned}Divide the interval into \( n=4 \) elements
Solution
Length of a single element:
\begin{aligned} h=\frac{b-a}{n}=1 \end{aligned}Position of individual nodes:
\begin{aligned} x_i=x_0+i\cdot h \end{aligned}We convert the equation \(y''(x)=2x\) using difference formulas:
\begin{aligned} &\frac{1}{h^2}\left(x_{i-1}-2 \cdot x_i+x_{i+1}\right)=2 x \\ &x_{i-1}-2 \cdot x_i+x_{i+1}=h^2 \cdot 2 x \end{aligned}For each node \(i=1,2,3,4\) we write a difference equation according to the above formula, and we also record the value of x for each node:
\begin{array}{lll} i=1 & x_0-2 \cdot x_1+x_2=h^2 \cdot 2 x_1 & x_1=x_0+h=4 \\ i=2 & x_1-2 \cdot x_2+x_3=h^2 \cdot 2 x_2 & x_2=x_0+2 h=5 \\ i=3 & x_2-2 \cdot x_3+x_4=h^2 \cdot 2 x_3 & x_3=x_0+3 h=6 \\ i=4 & x_3-2 \cdot x_4+x_5=h^2 \cdot 2 x_4 & x_4=x_0+4 h=7 \end{array}Consider the boundary conditions, also converting them into difference formulas:
\begin{array}{lll} y(a)=4 & x_0=4 & \\ y^{\prime}(b)=2 & \frac{1}{2 h}\left(-x_3+x_5\right)=2 & -x_3+x_5=4 h \end{array}We write down the above equations in matrix form \(A\cdot y = B\)
\( \left[\begin{array}{cccccc} 1 & -2 & 1 & 0 & 0 & 0 \\ 0 & 1 & -2 & 1 & 0 & 0 \\ 0 & 0 & 1 & -2 & 1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \end{array}\right] \cdot\left[\begin{array}{l} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{array}\right]=\left[\begin{array}{c} h^2 \cdot 2 \cdot x_1 \\ h^2 \cdot 2 \cdot x_2 \\ h^2 \cdot 2 \cdot x_3 \\ h^2 \cdot 2 \cdot x_4 \\ 4 \\ 4 \cdot h \end{array}\right]=\left[\begin{array}{c} 8 \\ 10 \\ 12 \\ 14 \\ 4 \\ 4 \end{array}\right] \)And finally, the solution (in this case obtained in Mathcad):
\( y=A^{-1} B=\left[\begin{array}{r} 4 \\ -31 \\ -58 \\ -75 \\ -80 \\ -71 \end{array}\right] \)In practice, we are only interested in the first 5 results, because the last one is actually outside the interval of interest \(i=5 -> x=8\)
The analytical solution of this differential equation obtained using classical methods for solving differential equations:
\( y_{a n}(x)=\frac{x^3}{3}-47 x+136 \)
The table shows the values along with the errors for each point
\( \begin{array}{|r|r|r|r|r|r|} \hline \mathrm{i} & x & y & y_a & \text { Absolute Error } & \text { Relative Error } \\ \hline 0 & 3 & 4 & 4 & 0 & 0.00 \% \\ \hline 1 & 4 & -31 & -30.667 & 0.333 & 1.09 \% \\ \hline 2 & 5 & -58 & -57.333 & 0.667 & 1.16 \% \\ \hline 3 & 6 & -75 & -74 & 1 & 1.35 \% \\ \hline 4 & 7 & -80 & -78.667 & 1.333 & 1.69 \% \\ \hline \end{array} \)If we divided the interval into more elements, the accuracy would be higher, but in such cases it would be necessary to use computational programs like Matlab