Edupanda » Technical Mechanics » 3D Statics - Equilibrium of Spatial Force System
3D Statics - Equilibrium of Spatial Force System
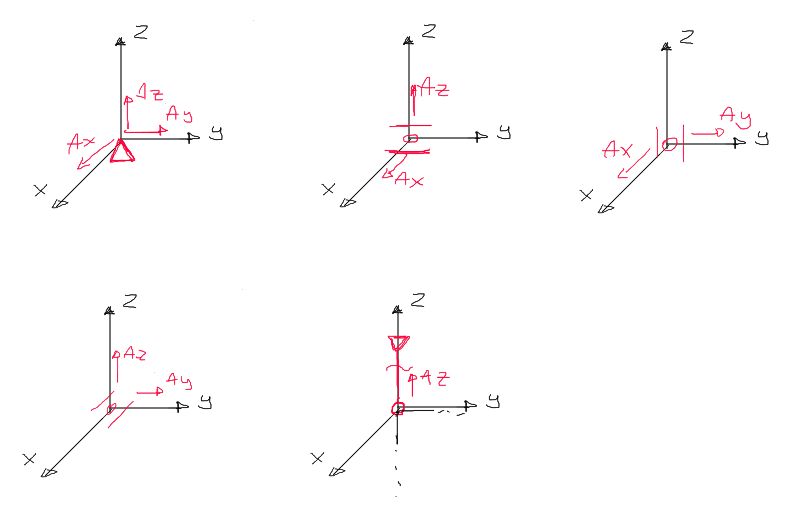
Sample supports
Equilibrium equations
\begin{aligned} & \Sigma F_x=0 \\ & \Sigma F_y=0 \\ & \Sigma F_z=0 \\ & \Sigma M_x=0 \\ & \Sigma M_y=0 \\ & \Sigma M_z=0 \end{aligned}
Example 1
Content
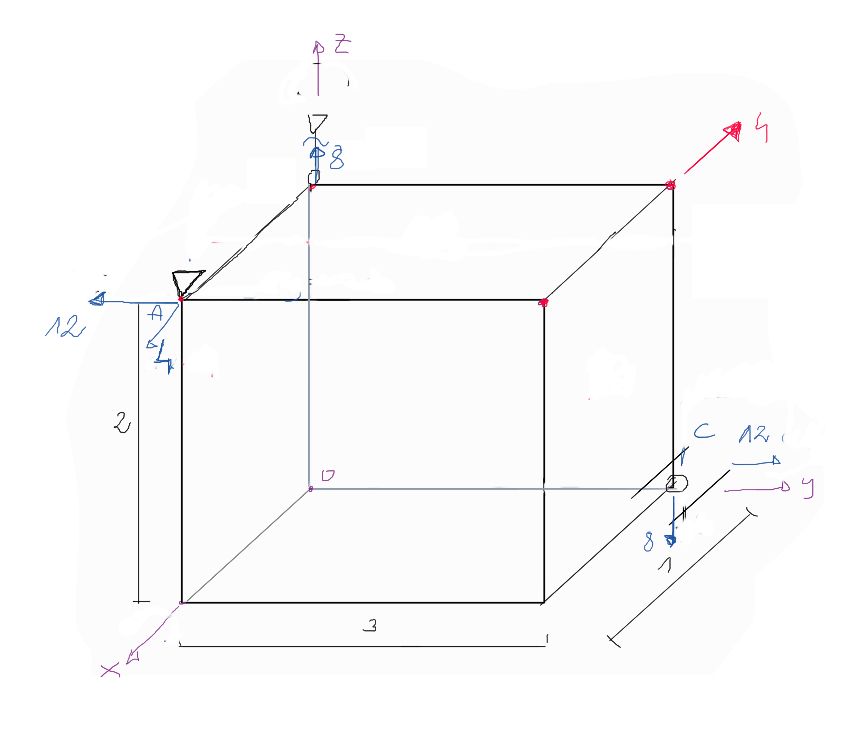
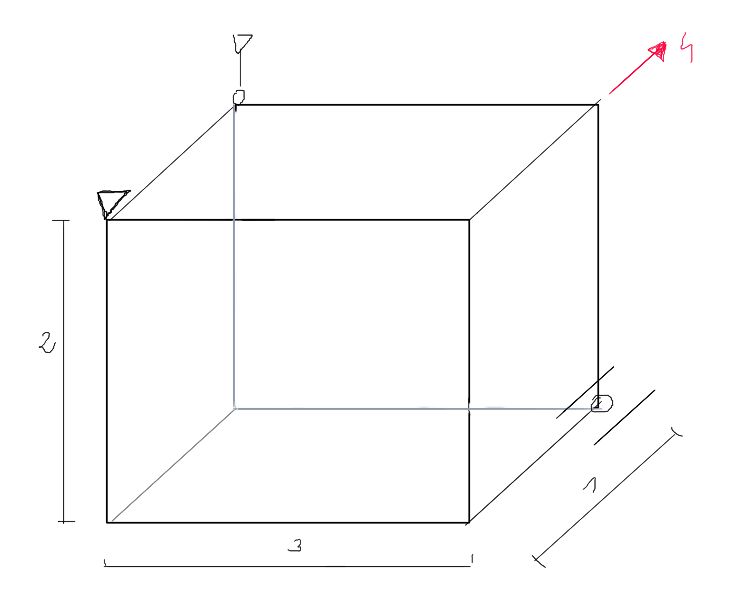
For the given system, determine the reactions
Solution
Release from constraints
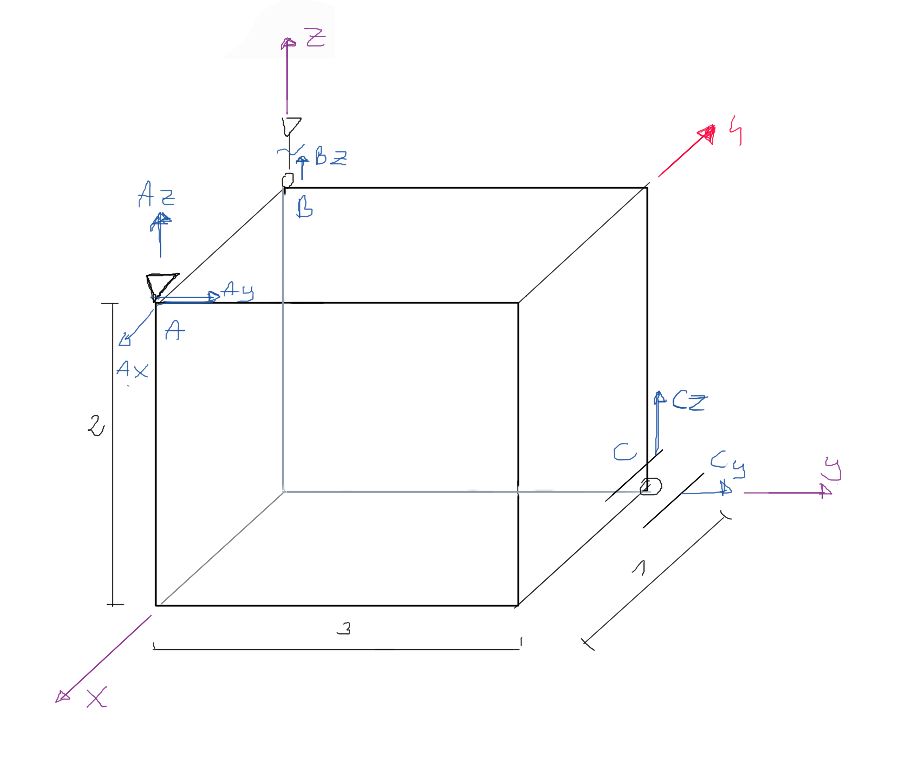
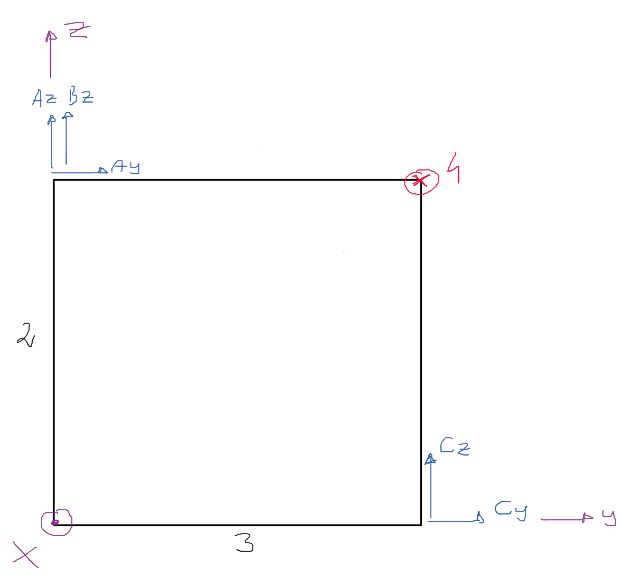
Sum of projections on the axes of the system:
\begin{aligned} & \Sigma F_x=0 \quad A_x-4=0 \quad A_x=4 \\ & \Sigma F_y=0 \quad A_y+C_y=0 \\ & \Sigma F_z=0 \quad A_z+B_z+C_z=0 \\ & \end{aligned}Sum of moments about the X axis
 \begin{aligned}
\Sigma M_x=0 \quad C_z \cdot 3-A_y \cdot 2=0
\end{aligned}
\begin{aligned}
\Sigma M_x=0 \quad C_z \cdot 3-A_y \cdot 2=0
\end{aligned}
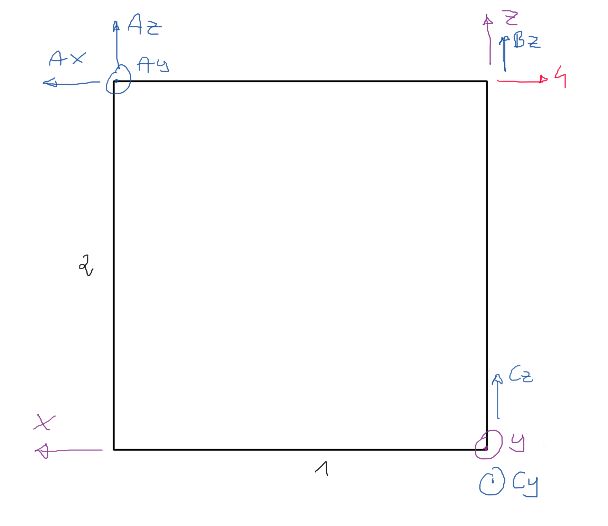
Sum of moments about the Y axis
 \begin{aligned}
\Sigma M_y=0 \quad-A_z \cdot 1+A_x \cdot 2-4 \cdot 2=0 \quad A_z=0
\end{aligned}
\begin{aligned}
\Sigma M_y=0 \quad-A_z \cdot 1+A_x \cdot 2-4 \cdot 2=0 \quad A_z=0
\end{aligned}
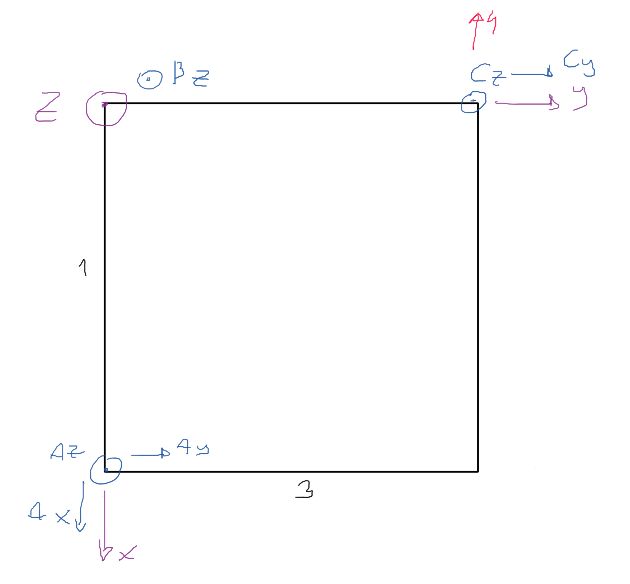
Sum of moments about the Z axis
 \begin{aligned}
\Sigma M_z=0 \quad A_y \cdot 1+4 \cdot 3=0 \quad A_y=-12
\end{aligned}
\begin{aligned}
\Sigma M_z=0 \quad A_y \cdot 1+4 \cdot 3=0 \quad A_y=-12
\end{aligned}
Substituting the calculated values into the previous equations:
\begin{aligned} &C_z \cdot 3-A_y \cdot 2=0 \quad C_z=\frac{2}{3} A_y=-8\\ &A_y+C_y=0 \quad C_y=-A_y=12 \end{aligned}Summary of results